线性代数进阶

矩阵变换

矩阵的标准型:相似变换(把矩阵看做线性映射)



矩阵的标准型:相合变换(二次型)




主成分分析(PCA)
PCA(Principal Component Analysis)是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降维。降维当然意味着信息的丢失,不过鉴于实际数据本身常常存在的相关性,我们可以想办法在降维的同时将信息的损失尽量降低。举个例子,假如某学籍数据有两列M和F,其中M列的取值是如何此学生为男性取值1,为女性取值0;而F列是学生为女性取值1,男性取值0。此时如果我们统计全部学籍数据,会发现对于任何一条记录来说,当M为1时F必定为0,反之当M为0时F必定为1。在这种情况下,我们将M或F去掉实际上没有任何信息的损失,因为只要保留一列就可以完全还原另一列。
选择不同的基可以对同样一组数据给出不同的表示,而且如果基的数量少于向量本身的维数,则可以达到降维的效果。但是我们还没有回答一个最最关键的问题:如何选择基才是最优的。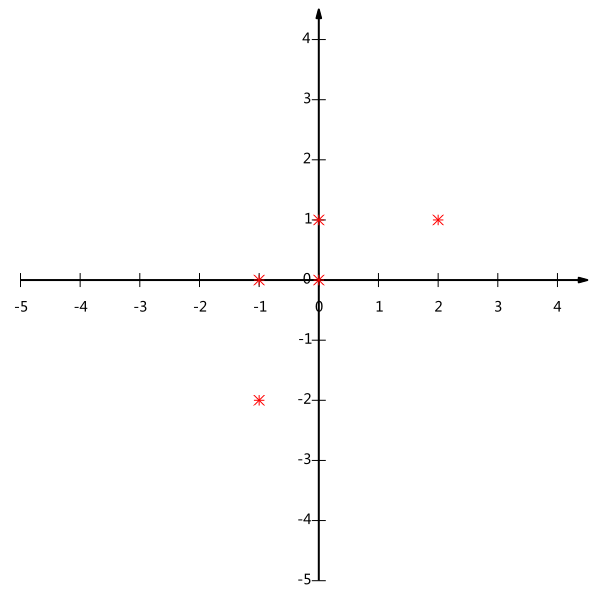
如图中如果想要将二维转化为一维,若想少丢失信息,则应将投影尽可能的分散。而这种分散程度,可以用数学上的方差来表述。
于是上面的问题被形式化表述为:寻找一个一维基,使得所有数据变换为这个基上的坐标表示后,方差值最大。
考虑三维降到二维问题。与之前相同,首先我们希望找到一个方向使得投影后方差最大,这样就完成了第一个方向的选择,继而我们选择第二个投影方向。直观上说,让两个字段尽可能表示更多的原始信息,我们是不希望它们之间存在(线性)相关性的,因为相关性意味着两个字段不是完全独立,必然存在重复表示的信息。数学上可以用两个字段的协方差表示其相关性。
至此,我们得到了降维问题的优化目标:将一组N维向量降为K维(K大于0,小于N),其目标是选择K个单位(模为1)正交基,使得原始数据变换到这组基上后,各字段两两间协方差为0,而字段的方差则尽可能大(在正交的约束下,取最大的K个方差)。
上面我们导出了优化目标,但是这个目标似乎不能直接作为操作指南(或者说算法),因为它只说要什么,但根本没有说怎么做。所以我们要继续在数学上研究计算方案。
根据上述推导,我们发现要达到优化目前,等价于将协方差矩阵对角化:即除对角线外的其它元素化为0,并且在对角线上将元素按大小从上到下排列,这样我们就达到了优化目的。




最后需要说明的是,PCA是一种无参数技术,也就是说面对同样的数据,如果不考虑清洗,谁来做结果都一样,没有主观参数的介入,所以PCA便于通用实现,但是本身无法个性化的优化。
(奇异值分解)SVD

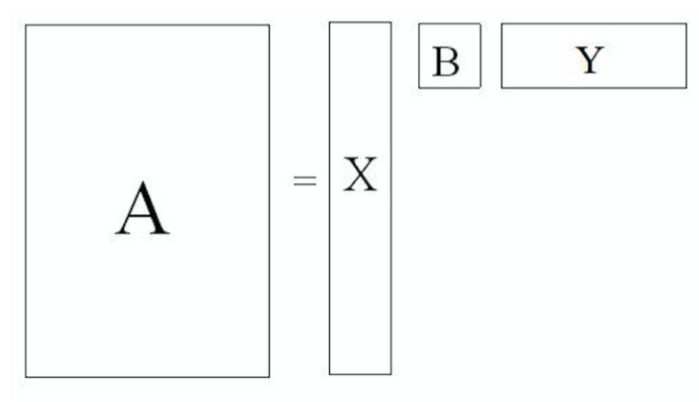

SVD与PCA
我们讲到要用PCA降维,需要找到样本协方差矩阵的最大的k个特征向量,然后用这最大的k个特征向量张成的矩阵来做低维投影降维。 SVD也可以得到协方差矩阵最大的k个特征向量张成的矩阵。 就是说,PCA算法可以不用做特征分解,而是做SVD来完成。
凸优化




最小二乘法是经常使用的优化算法。

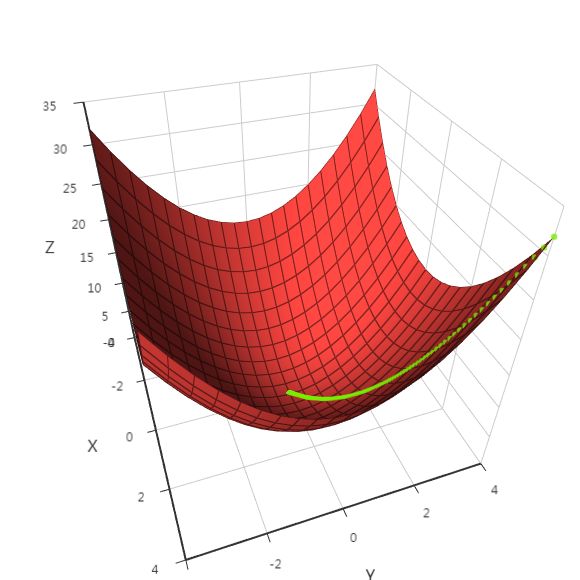
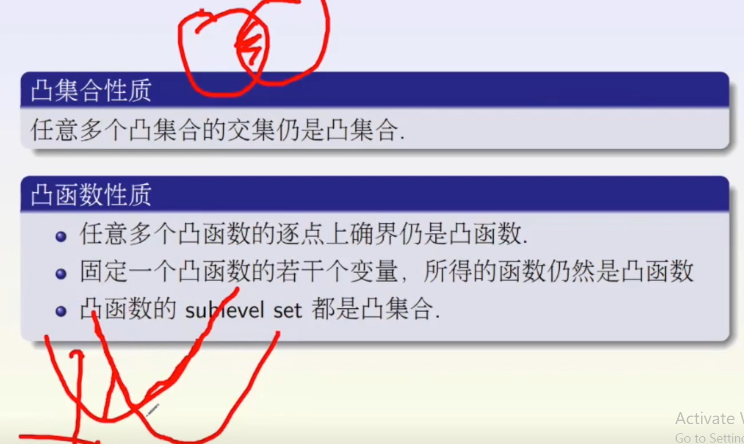
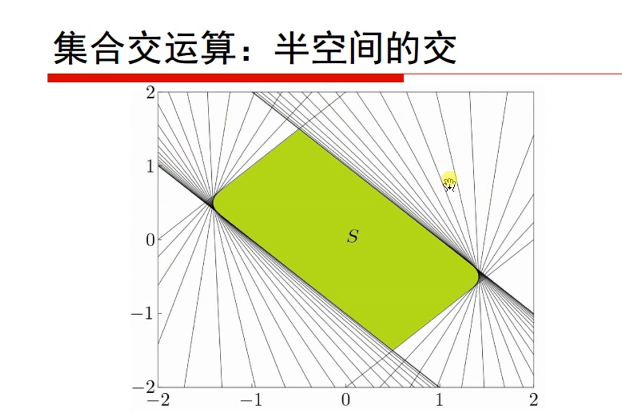
对于目标函数,我们限定是凸函数;对于优化变量的可行域(注意,还要包括目标函数定义域的约束),我们限定它是凸集。同时满足这两个限制条件的最优化问题称为凸优化问题,这类问题有一个非常好性质,那就是局部最优解一定是全局最优解。
凸集:
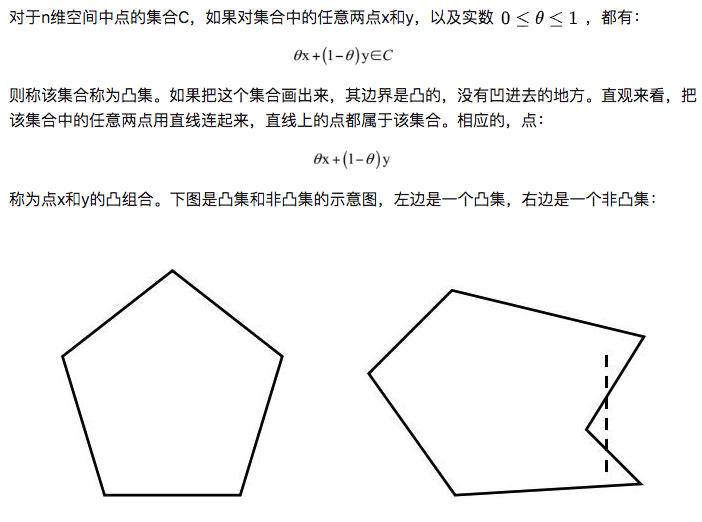



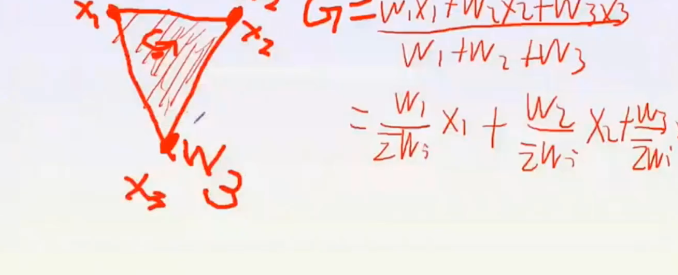






优化问题举例:EM算法简介与混合高斯模型







第一步(E):如果这个混合模型中,每一次的输出我们知道它是从哪一个模型里边出来的就好了
第二步(M):最大化似然函数
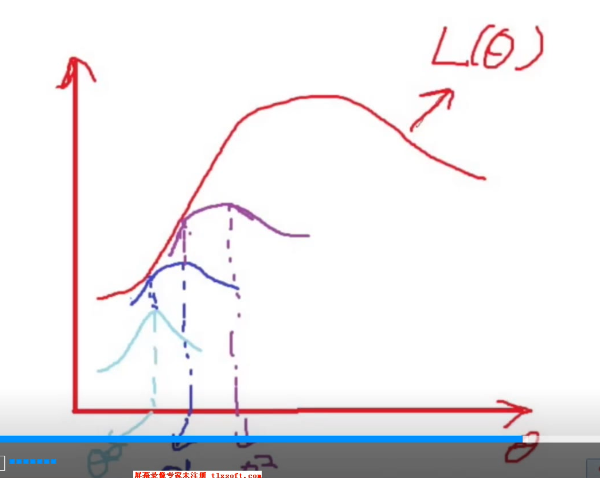
逐次逼近最优解。
凸优化进阶
机器学习与优化
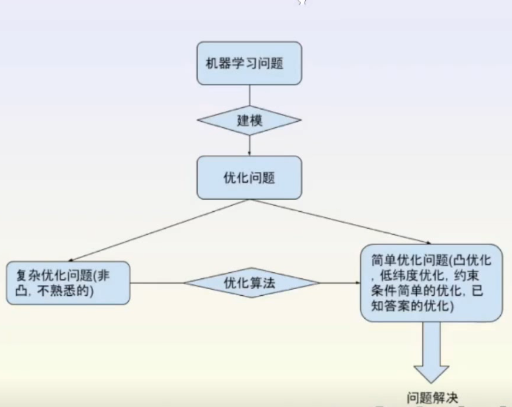
共轭函数与对偶方法

给定一个优化问题,如果比较复杂,可以转化为优化问题的对偶问题。

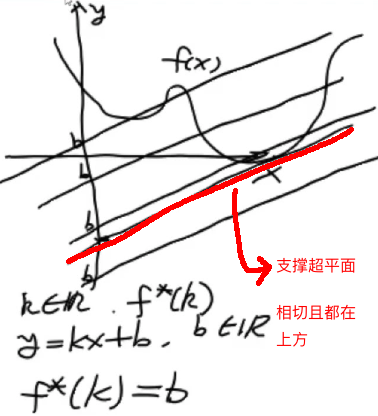
勒让德(Legendre)变化的理解:函数上境图的支撑超平面的截距。
对偶(共轭)函数抓住了原来函数的一些性质,没有抓住全部性质,抓住了原来函数凸闭包的性质。非凸函数的凸闭包函数是最接近其性质的凸函数,所以可以拿来做近似。第一个结论告诉我勒让德变换抓的是凸包的性质,第二个性质告诉我们,如果是凸函数了。变成共轭函数了没有丢失信息,再做一次变换还能变回来。
第三点说明对于一般的函数,共轭变换是丢失了一部分信息的。

第二点说的就是几何性质。
对偶问题:拉格朗日对偶问题

对于没有约束条件的问题,可以使用牛顿法。对于有约束条件的问题,最优解可能不在可行域里,这时就不太好解了。

当对一群线性函数取逐点极小值的时候,得到的是一个凹函数。所以g函数是一个凹函数。其中x属于全部定义域,是没有约束条件的,这样再做就比较简单。

我们将一个待求函数比较简单但约束条件比较复杂得问题转换为了一个待求函数比较复杂但约束条件比较简单的问题。把问题的复杂性转化到了函数里面去。待求函数不管凸的凹的可以用牛顿法去做逼近。
那转化后的问题与原问题有什么关系呢?
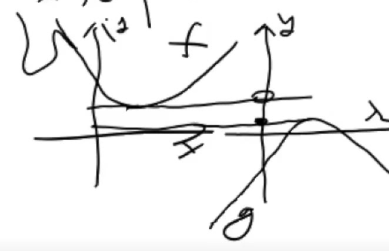
用g的上界提供了原问题的下界。

d是g的最大值,p是f的最小值。
强对偶性条件

凸优化问题比较容易去求解,但是为什么还需要求对偶变化呢,是因为约束条件比较复杂。需要简化。
当你是对偶问题时,在凸性上一定是变好的,但是不一定能抓住原来问题的所有性质。






一些概念

琴生不等式:


上确界(Supremum):一个集合的最小上界, 数学符号sups
下确界(greatest lower boundinf):一个集合的最大下界,数学符号inf
上确界与最大值:上确界类似于最大值,但是和最大值不同的是,最大值有时候会遇到无法取到的情况。比如x∈R,x<2这样的情况下就不存在一个确定的最大值。但是可以确定上确界为2。


a,x都是向量,b是常数。

简单来说仿射变换就是线性变换加平移。线性变化中原点还在原点,但仿射变换后,原点就移动了。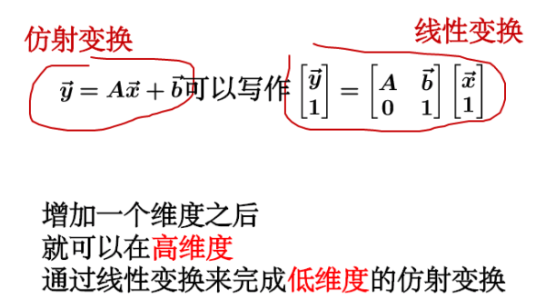
如何通俗地讲解「仿射变换」这个概念? - 马同学的回答 - 知乎
https://www.zhihu.com/question/20666664/answer/157400568
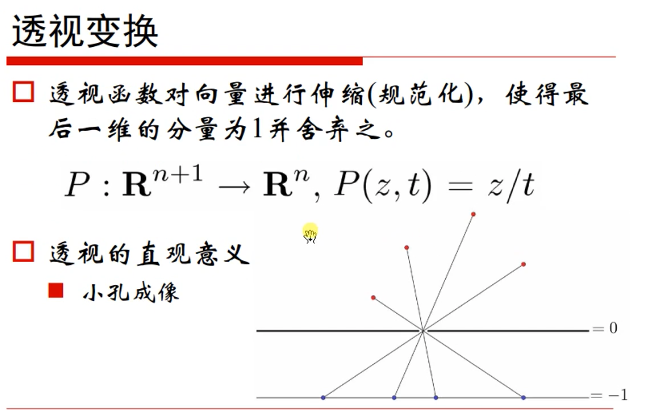
将前z维每一项都除以最后一维t,将最后一项t舍弃。


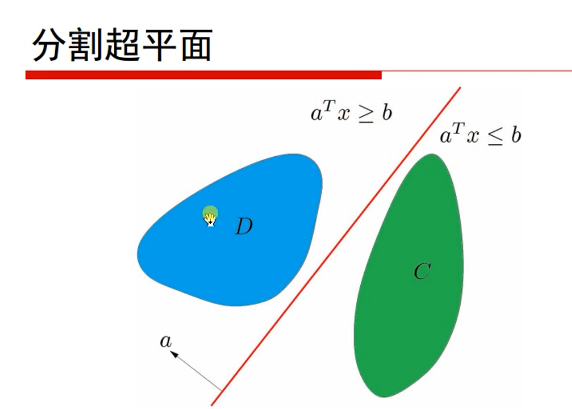


支持向量机(SVM)


分割使用的是n-1维的超平面。

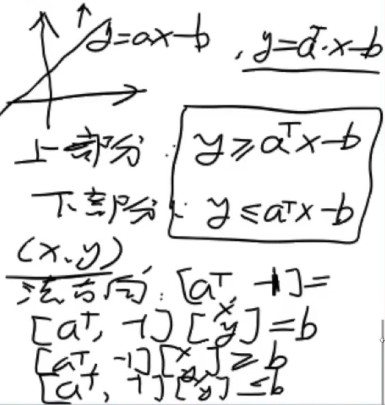

等式条件定义了一个球面,球面不是一个凸集合。
此时把支持向量机问题转化为了一个凸优化问题。







允许c和d有一部分交叉。
或者使用核方法,将维度增加,再进行划分。

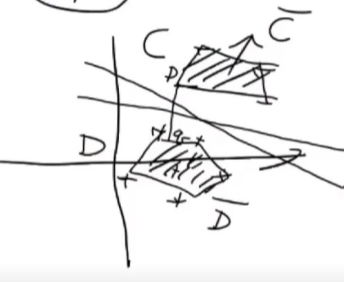
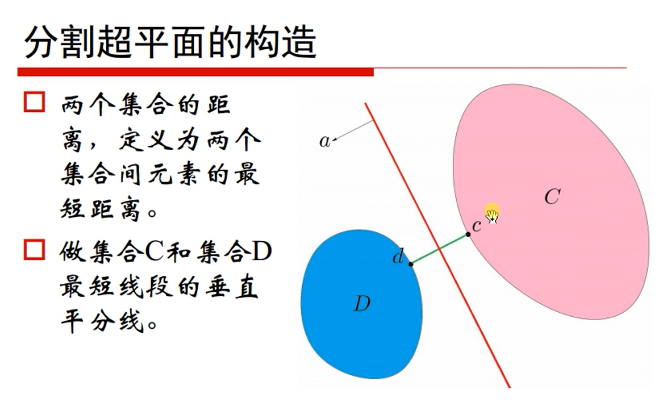
C抜D抜离得最近的两个点的垂直平分线。

压缩感知与图像处理






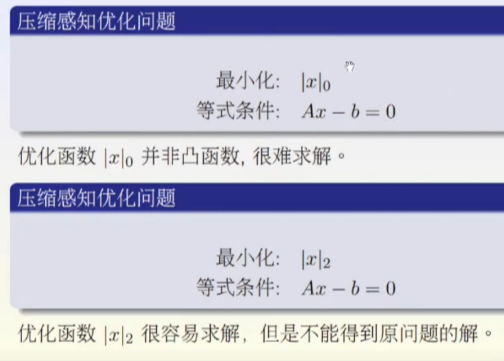
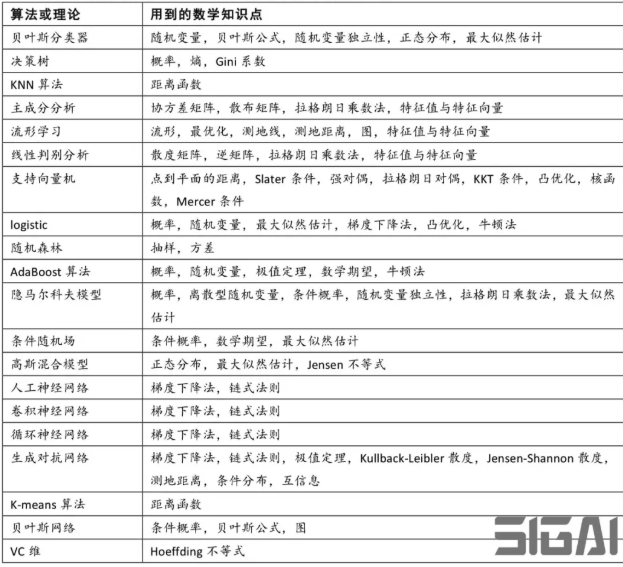
算法和理论与数学知识点