机器学习基础
见李宏毅第0课。
得分函数
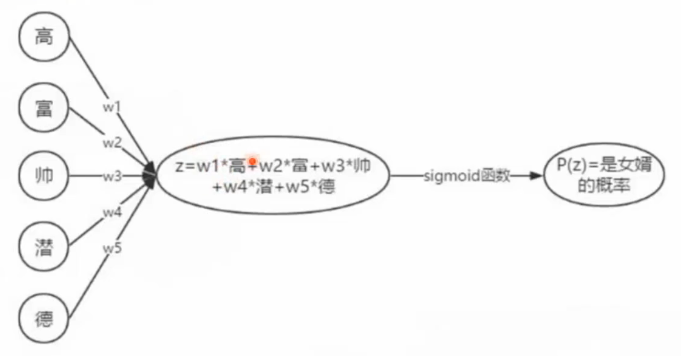
权重需要训练得到。
损失函数最优化
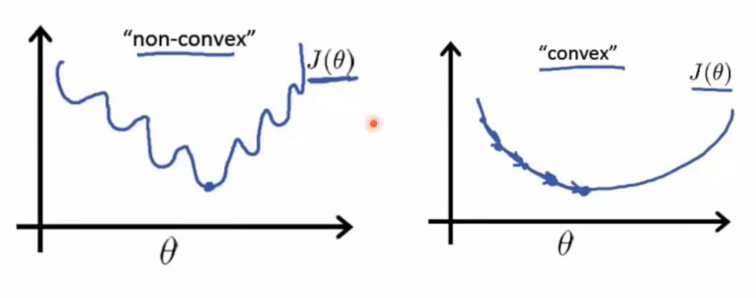
左边是非凸函数,右边是凸函数。通过优化损失函数来调整权值。
凸函数
琴生不等式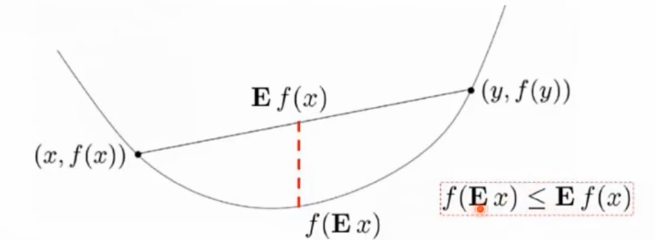
微积分基础

梯度是一个点上升最快的方向。
梯度下降法。
极限
通俗语言适合于说给对方听,数学记号适合于写给对方看,精确描述比较啰嗦但是非常精确不会造成误解,主要用于证明。不会出错。
无穷小的阶数。


微分学





求导用链式法则。
积分学


泰勒级数。


牛顿法与梯度下降法



为什么不用牛顿法:
原因一:牛顿法需要用到梯度和Hessian矩阵,这两个都难以求解。因为很难写出深度神经网络拟合函数的表达式,遑论直接得到其梯度表达式,更不要说得到基于梯度的Hessian矩阵了。
原因二:即使可以得到梯度和Hessian矩阵,当输入向量的维度NNN较大时,Hessian矩阵的大小是N×NN×NN\times N,所需要的内存非常大。
原因三:在高维非凸优化问题中,鞍点相对于局部最小值的数量非常多,而且鞍点处的损失值相对于局部最小值处也比较大。而二阶优化算法是寻找梯度为0的点,所以很容易陷入鞍点。


为什么研究凸函数,凸优化?


概率与统计基础

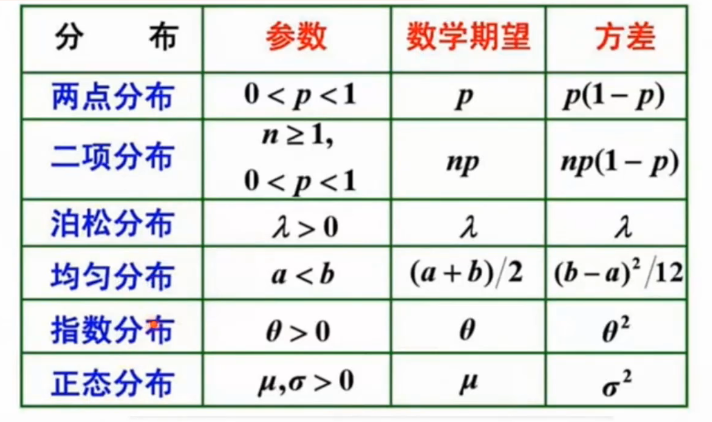
统计问题是概率问题的逆向工程。
概率问题是已知总体的情况,求一次的概率。统计问题则是根据样本的情况反推总体的情况。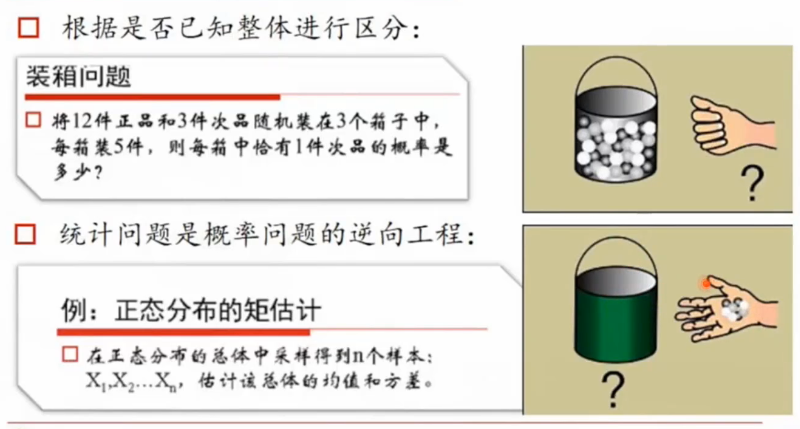
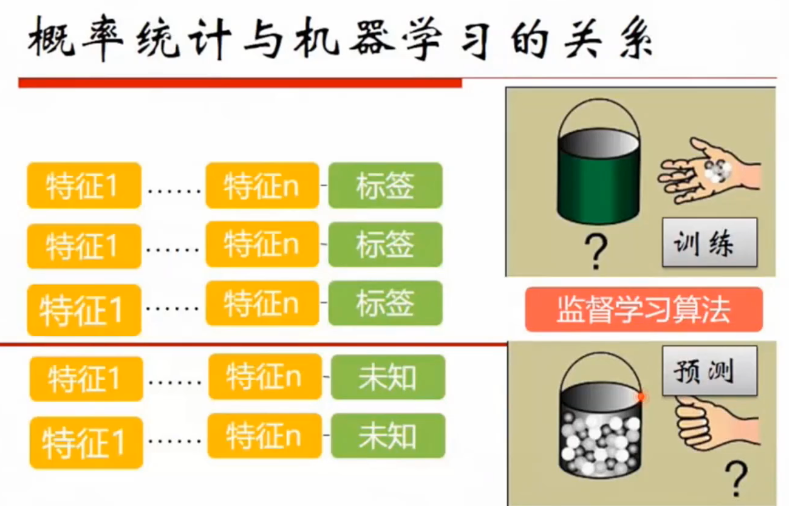
概率统计与机器学习的关系
概率统计与机器学习天然相关,训练的过程可以看做是统计过程,预测过程可以看做是概率过程。预测分类就是选择一个概率最大的分类。
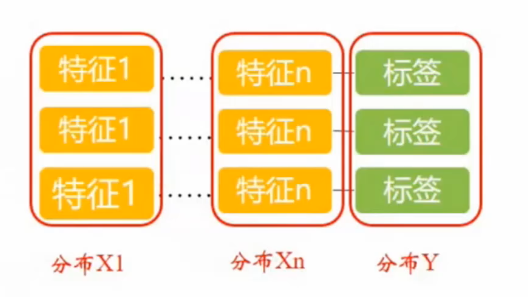
可以观察各个特征的分布以及标签的分布,筛选出相关性强的特征。
- 可基于各个分布的特性来评估模型和样本。
- 统计估计的是分布,机器学习训练出来的是模型,模型可能包含了很多的分布。
- 训练与预测过程的一个核心评价指标就是模型的误差
- 误差本身就可以使概率形式,与概率紧密相关。
- 对误差的不同定义方式就演化成了不同损失函数的定义方式。
- 机器学习是概率与统计的进阶版本。(不严谨的说法)
方差
协方差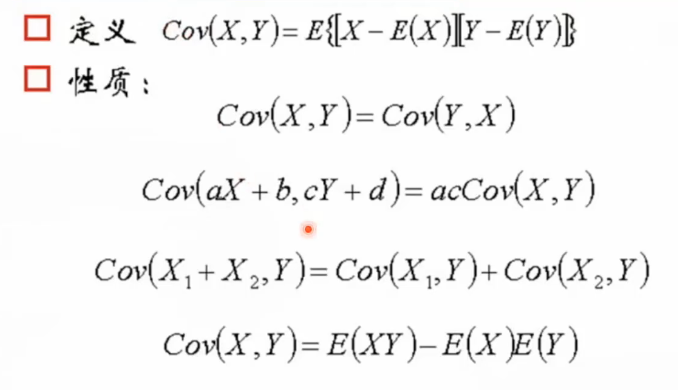
可评估两个分布之间的关系。定义公式几何意义:协方差可以理解成特征进行预处理之后(去均值化,机器学习里比较重要的一个数据预处理的方法)对应的向量的几何的内积。协方差是评价两个变量的线性关系。如果是非线性关系,评价不出来。
相关系数是研究变量之间线性相关程度地量。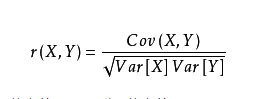
var是方差。
概率论






先验——根据若干年的统计(经验)或者气候(常识),某地方下雨(因)的概率;
似然/类条件概率——在下雨(因)的情况下,观测到了乌云(果)的概率,即原因已知时,结果出现的概率;
后验——根据天上有乌云(果),得到的下雨(因)的概率,即给定结果估计原因的概率;
x:观察得到的结果。
θ:决定数据分布的原因。

矩:
其中t是一个实数,i是虚数单位,E表示期望值。此乃原点矩。E((X-0)^n)中心矩就是-μ。
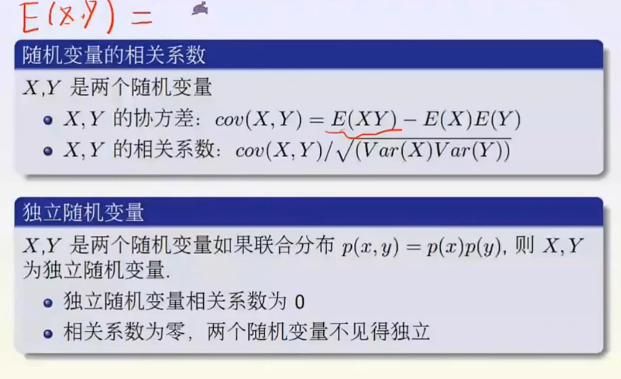
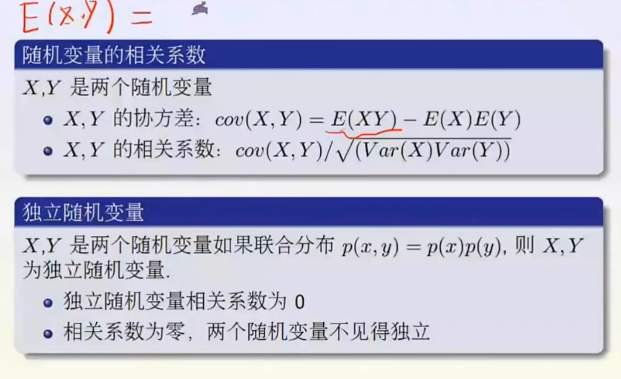

即大部分都分布在均值周围。








没法研究随机变量就研究其特征函数。
当一个分布不是常见的分布时,根据大数定理,反复做实验就可以得到其期望和方差。

大数定理是告诉我们趋近一个数,中心极限定理是告诉我们以何种方式趋近一个数。一个正态分布。
参数估计(统计学)

点估计
利用样本来估计总体分布,总体分布的参数很多情况下是未知的。如均值μ、方差\sigma ^{2} 、泊松分布的λ、二项分布的比例π,其它分布还会有更多的未知参数,需要通过样本进行相应的估计,这种估计值就是点估计。
矩估计





极大似然估计


可以把概率密度看作是θ和x的联合概率密度,把x固定,那么概率密度最大的地方就是θ最可能的地方。
不是概率是因为相加起来和不等于1,类似于概率是因为数值大小是有意义的,代表了可能性的大小。
如何通俗地理解概率论中的「极大似然估计法」? - 马同学的回答 - 知乎
https://www.zhihu.com/question/24124998/answer/242682386
简单来说,极大似然函数就是通过样本来求使得概率(似然)为最大的那个θ值。似然越大,就越有可能是这个θ。所以目的就是让似然函数最大就完事了,然后可以通过对θ的梯度下降法,使得似然函数求最大,也就是损失函数为负的似然函数求最小。
点估计的评判准则

区间估计
对于未知参数,点估计值只是一个近似值,会存在或大或小误差,这时给一个范围可能是更合适,也是更可信的。比如从北京到张家界旅游5天,你恐怕不能准确说出要花多少钱,但你可以给出一个范围,比如10000—13000,你会觉得比较可信。如果给的范围太大,比如10000—30000,虽然可信度更高一些,但这么大的范围参考意义不大;如果给的范围很小,如10000——10500,则准确性提高了,但可信度就似乎不会很高。找到一个合适的估值范围,这是置信区间要解决的问题。

线性代数基础
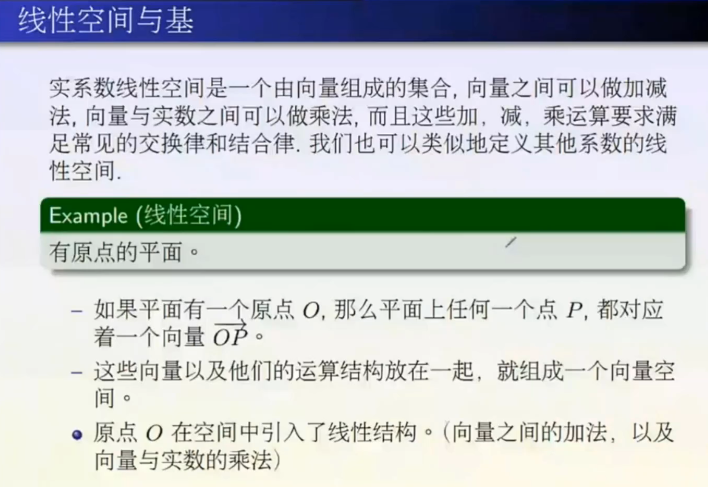



(1)保持加法(2)保持乘法。
线性映射是最简单的研究对象,用线性映射去逼近别的东西。
线性变换与矩阵的关系,对任何向量x进行线性变换T的结果向量,是一个对基向量组进行线性变换T之后的新向量组的一个线性组合,系数没变。
只需要知道两个基向量i向量和j向量转换之后的的结果,而不用知道转换本身,我们就能推导出二维空间中所有向量转换之后的结果。
Ax的几何意义
矩阵乘向量,列向量的线性组合。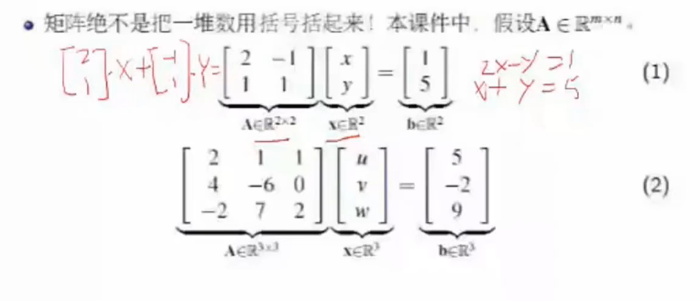
svd的几何意义。
一个很重要的降维算法。
矩阵乘法在计算中的优势
- 将很多for循环写成矩阵或者向量乘法的方式。
- 矩阵计算模块在底层有优化。
- numpy进行矩阵运算很快。