Trie树
实现搜索引擎的搜索关键词提示功能
什么是Trie树
Trie树也叫字典树,是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。
例如有6个字符串,分别是how,hi,her,hello,so,see。想要在里面多次查找某个字符串是否存在。如果每次查找都是依次匹配,效率就比较低。可以对6个字符串进行预处理组织成Trie树结构,之后每次查找都是在Trie树中进行匹配查找。Trie树的本质就是利用字符串之间的公共前缀,将重复的前缀合并在一起。
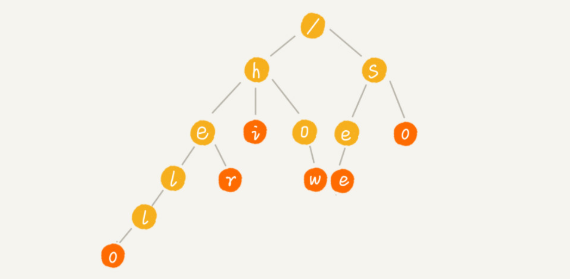
根节点不包含任何信息,每个节点表示一个字符串中的字符,从根节点到红色节点的一条路径表示一个字符串(注意:红色节点并不都是叶子节点)。
字符串的构造过程如下,Trie树构造的每一步,都相当于往Trie树中插入一个字符串。当所有字符串都插入完成后,Trie树就构造好了。
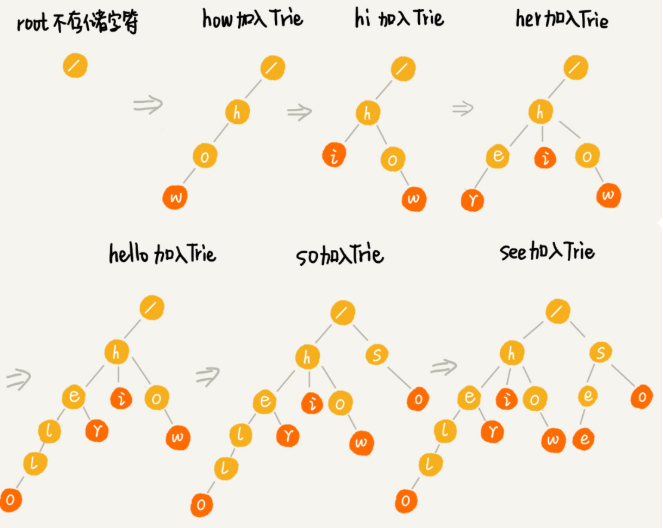
在进行查找时就是从根节点开始,但是不一定一路到叶子节点。可能提前终止。
实现Trie树
Trie树主要有两个操作,一个是将字符串集合构造成Trie树。这个就是将字符串插入到Trie树的过程。另一个是在Trie树中查询一个字符串。
存储一个Trie树
一种经典的存储方式是借助散列表的思想,通过下标与字符–映射的数组来存储子节点的指针。
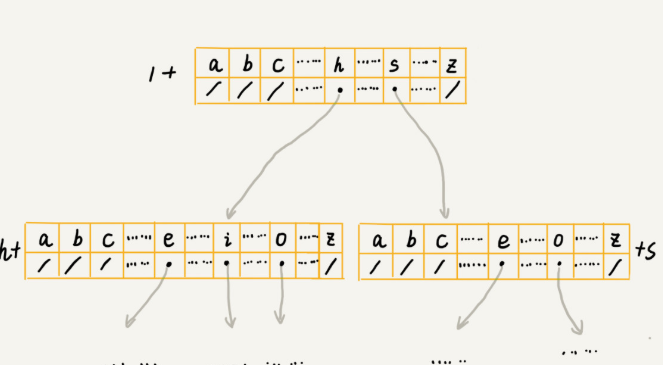
在Trie树中查找某个字符串的时间复杂分析:
在一组字符串中频繁查询某些字符串,用Trie树会非常高效,构建Trie树的过程需要扫描所有的字符串,时间复杂度是O(n)。一旦构建成功之后,后续的查询操作会非常高效。
构建好Trie树后,在其中查找字符串的时间复杂度是O(k),k表示要查找的字符串的长度。
Trie树内存分析:
在Trie树实现时,用到数组来存储一个节点的子节点指针,如果字符串中包含从a到z这26个字符,则每个节点都要存储一个长度为26的数组,即便一个节点只有很少的子节点,远少于26个,也要维护一个长度为26的数组。如果字符串中不仅包含小写字母,还包含大写字母、数字、中文,那需要的存储空间就更加多了。即Trie树不旦不能节省内存,还有可能会浪费更多的内存。
Trie树与散列表、红黑树的比较
- 字符串中包含的字符集不能太大。我们前面讲到,如果字符集太大,那存储空间可能就会浪费很多。即便可以优化,但也要付出牺牲查询、插入效率的代价。
- 要求字符串的前缀重合比较多,不然空间消耗会变大很多。
- 如果要用Trie树解决问题,那就要自己从零开始实现一个Trie树,还要保证没有bug,这个在工程上是将简单问题复杂化,除非必须,一般不建议这样做。
- 通过指针串起来的数据块是不连续的,而Trie树中用到了指针,所以,对缓存并不友好,性能上会打个折扣。
在工程中,更倾向于使用散列表或者红黑树,因为这两种数据结构都不需要自己去实现,Trie树更适合于查找前缀匹配的字符串,比如搜索引擎的提示框。
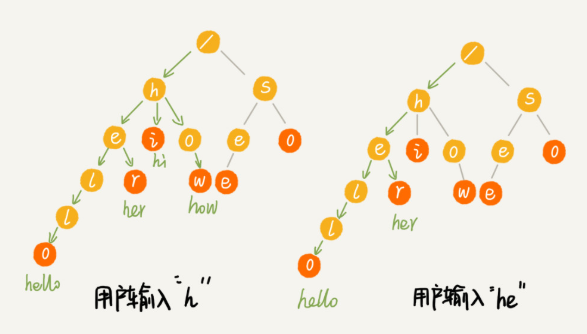
以及输入法的自动补全功能、IDE代码自动补全等。
AC自动机
用来实现敏感词过滤
BF、RK、BM、KMP算法都是单模式匹配算法,Trie树是多模式串匹配算法。
单模式串匹配算法,是在一个模式串和一个主串之间进行匹配,也就是在一个主串中查找一个模式串。多模式串匹配算法,就是在多个模式串和一个主串之间做匹配,就是在一个主串中查找多个模式串。
经典的多模式串匹配算法:AC自动机
Trie树跟AC自动机之间的关系,就像单串匹配中朴素的串匹配跟KMP算法之间的关系。AC自动机实际上就是在Trie树上,加了类似KMP的next数组,只是next数组是构建在树上的。
AC自动机的构建包含两个操作:1.将多个模式串构建成Trie树 2.在Trie树上构建失败指针(相当于KMP中失效函数next数组)