字符串匹配算法 KMP
BM算法是工程中非常常用的一种高效字符串匹配算法,是最高效最常用的字符串匹配算法。在所有字符串匹配算法中,最知名的非KMP算法莫属。
KMP算法基本原理
KMP算法的核心思想与BM算法非常相近。在模式串与主串匹配过程中,当遇到不可匹配的字符时,通过找到一些规律将模式串往后多滑动几位,跳过肯定不会匹配的情况。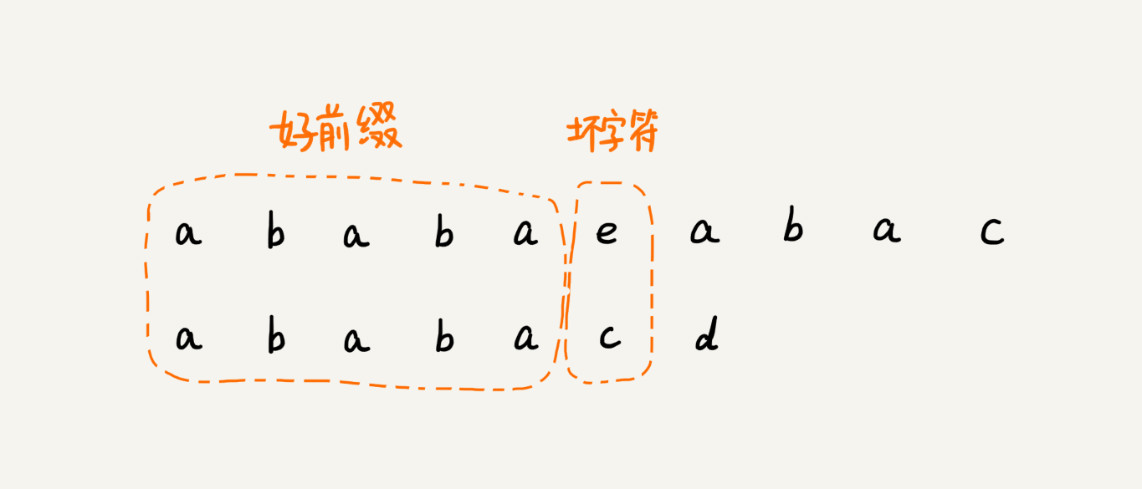
当遇到坏字符的时候,就要把模式串往后滑动,在滑动的过程中,只要模式串和好前缀有上下重合,前面几个字符的比较,就相当于拿好前缀的后缀子串,跟模式串的前缀子串在比较。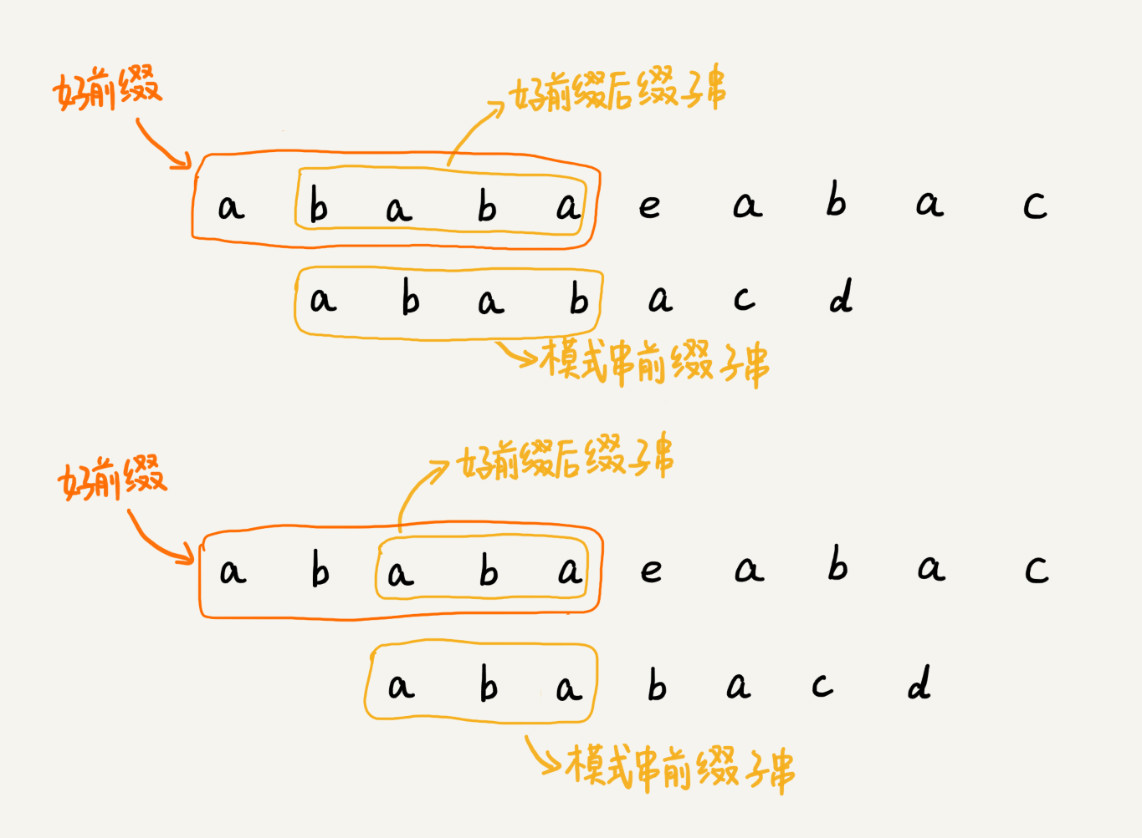
KMP算法就是在试图寻找一种规律: 在模式串和主串匹配的过程中,当遇到坏字符后,对于已经比对过的好前缀,找到一种规律,将模式串一次性滑动很多位。

求好前缀的最长可匹配前缀和后缀自串不涉及主串,只需要通过模式串本身就能求解。KMP算法也可以提前构建一个数组,用来存储模式串中每个前缀(有可能是好前缀)的最长可匹配前缀自串的结尾字符下标。把这个数组定义为next数组,又叫失效函数。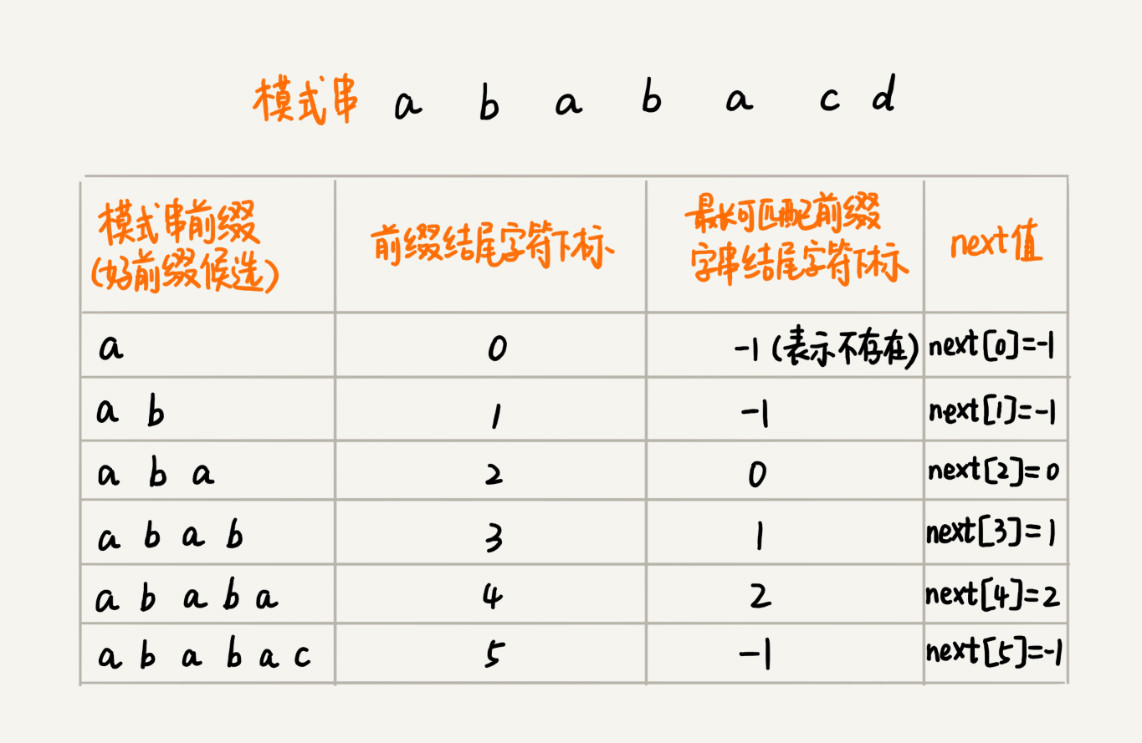
失效函数计算方法
最复杂的部分就是next数组计算。
最简单也最低效的是像👆一样依次遍历。
如何更好的理解和掌握 KMP 算法? - 逍遥行的回答 - 知乎
https://www.zhihu.com/question/21923021/answer/37475572
在计算next[i]时,前面的next[0],next[1],….,next[i-1]已经计算出来了,利用已经计算出来的next值,可以快速推导出next[i]的值。
例子:
abababzabababa
列个表计算一下:
对子字符串 abababzababab 来说,前缀有 a, ab, aba, abab, ababa, ababab, abababz, …后缀有 b, ab, bab, abab, babab, ababab, zababab, …所以子字符串 abababzababab 前缀后缀最大匹配了 6 个(ababab),容易看出次大匹配了 4 个(abab),更仔细地观察可以发现,次大匹配的前缀后缀只可能在 ababab 中,所以次大匹配数就是 ababab 的最大匹配数。
来计算 ? 的值:既然末尾字母不是 z,那么就不能直接 6+1=7 了,回退到次大匹配 abab,刚好 abab 之后的 a 与末尾的 a 匹配,所以 ? 处的最大匹配数为 5。
KMP算法复杂度分析
空间复杂度:
KMP算法只需要一个额外的next数组,数组的大小跟模式串相同。所以空间复杂度是O(m),m表示模式串的长度。
时间复杂度:
时间复杂度包括两部分,第一部分是构建next数组,第二部分是借助next数组匹配。
时间复杂度为O(m+n)