熵

https://www.jianshu.com/p/09b70253c840
完美解释交叉熵

随机变量

包含不确定性的变量称为随机变量，统计学就是研究这类不确定性变量的工具。刻画随机变量最有力的一个工具就是它的概率分布。有了概率分布，我们可以说对一个随机变量有了完全的掌握，因为我们可以知道它可能取哪些值，某个值的概率是多少。

什么是熵

概率分布是对随机变量的刻画，不同的随机变量有着相同或不同的概率分布，熵，就是对不同概率分布的刻画！本质上，是为了描述不确定的程度，并以此对不同的概率分布进行比较。

如果我们知道一枚硬币抛出后正面朝上概率为0.8，要比知道概率为0.5，更容易猜对硬币抛出后哪面朝上。即0.8的概率分布比0.5的概率分布对我们来说，具有更大的信息量。

需要的是一个定量的指标，来衡量概率分布的不确定性。这个指标就是熵。

熵的数学表达

以抛硬币为例，我们看正面这个取值。可以看到，取正面的概率越大，则不确定性就越小。即概率越大，不确定性越小。能够表达出概率越大，不确定性越小的表达式就是：
-logP，图像如下：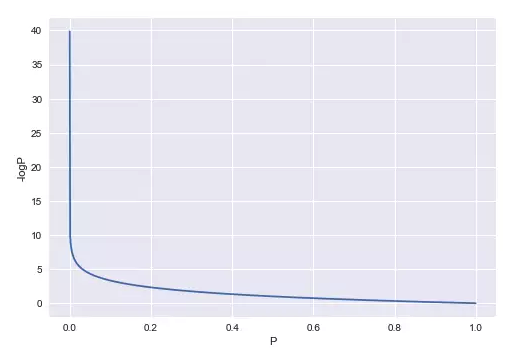

图中的纵轴为-logP，横轴为P。

-logP只是衡量了某个概率的不确定性，对于抛硬币，是正面的不确定性小了，那是反面的不确定性就大了。所以衡量一个概率的分布的不确定性，就要综合衡量所有概率表达的不确定性，也就是求一个概率分部综合的不确定性。熵的表达式即为：-∑PlogP

这个指标可以理解成概率分布的不确定性的期望值。这个值越大，表示该概率分布不确定性越大。它为我们人类提供的“信息”就越小，我们越难利用这个概率分布做出一个正确的判断。从这个角度，我们可以看到，熵是对概率分布信息含量的衡量，这与它是不确定性的衡量，其实是两种解读方式而已。

从另一个角度理解熵

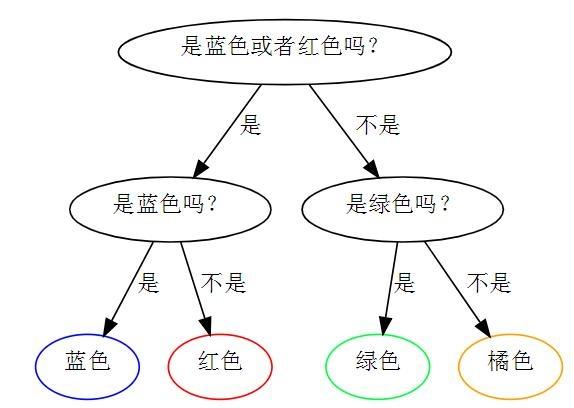
上图例中，每种颜色的概率都是1/4。此时的最优策略。

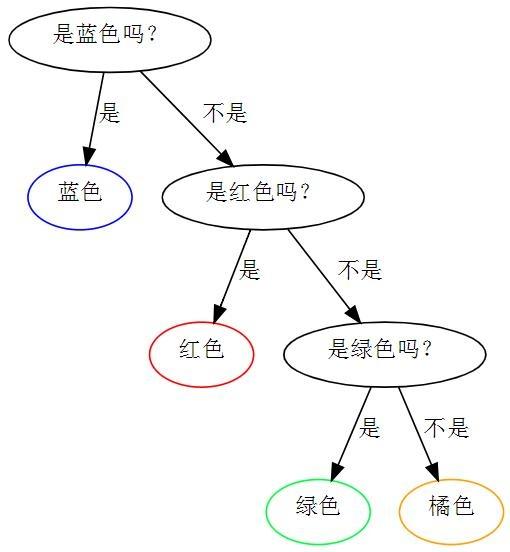
上图为1/8绿色, 1/8 橘色, 1/4 红色, 1/2 蓝色时的最优策略。

对于同一问题，目标是问最少次数的问题，就能得到正确的答案。在这个问题中, 问题个数的期望是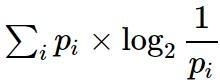

即为熵。
第一幅图的熵为 1/4(机率) 2道题目 4颗球 = 2，平均需要问两道题目才能找出不同颜色的球，也就是说期望值为2，就是熵。
第二幅图为1/2×1+1/4×2+1/8×3+1/8×3=1.75。
极端情况下全是一种颜色，就不用问问题，熵为0。

熵的意义就是在最优化策略下, 猜到颜色所需要的问题的个数。也就是一种情况下，只对应一个熵。在不同的情况中，熵越大，需要问的东西越多，说明其不确定性大，熵越小，需要判断的次数就越少。

伯努利分布的熵

抛硬币即为伯努利分布，它的熵为：H(p) = -plogp -(1-p)log(1-p)

画出来即为下图：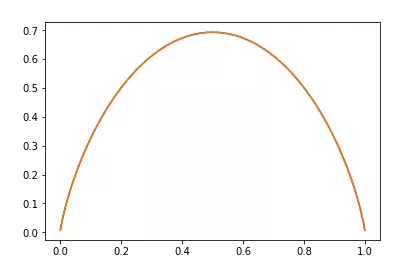

当p=0.5时，熵最大，因为此时硬币朝上朝下完全是随机的，不确定性最大。在两侧当其中一面向上的概率为1时，则完全没有不确定性。所以熵就是0。熵越大，不确定性越大，熵越小，信息越多。所以熵越小越好，可以把熵看做是优化的目标。

事实上方差可以用来描述变量变化程度，和熵有一致性，方差越大，不确定性就越大，熵就越大。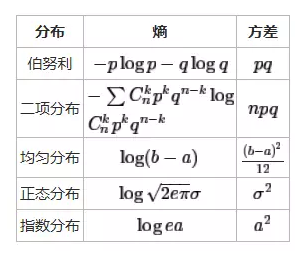

联合熵

联合熵与联合概率分布有关，对于随机变量X和Y，二者的联合概率分布为p(x,y),则这个联合概率分布的熵就叫做联合熵：
H(x,y) = -Σp(x,y)log(p(x,y))

H(x,y)肯定是大于等于H(x)或H(y)的。仅当X没有不确定性时，比如永远是正面朝上，此时，在Y的基础上联合X，并没有引入新的不确定性，所以，H(x,y)=H(y)。

条件熵

x,y的联合熵大于等于x和y单独的熵，对于y来说，引入的x增大了熵，那么，衡量x的引入增加了多大的熵呢，这就是条件熵。
H(x|y) = H(x,y) - H(y)

注意H(x|y)叫做条件熵，它可不是条件概率p(x|y)的熵。因为p(x|y)不是一个概率分布。

条件熵的计算，和条件概率还是有点关系的。
H(x|y) = - Σp(x,y)log(p(x|y))

条件熵是在Y上引入X后增加的不确定性，从感觉上，增加的不确定性无论如何不可能大于X本身自有的不确定性，也就是：
H(x|y) <= H(x) 仅当x，y相互独立时，等号才成立。

李航 信息增益

当熵和条件熵中的概率有数据统计（特别是极大似然估计）得到时，所对应的熵与条件熵分别称为经验熵和经验条件熵。此时如果有0概率，令0log0=0

信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。

特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即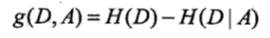

一般地，熵H(Y)与条件熵H(Y|X)之差称为互信息。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。详见决策树个人总结。

相对熵（又叫互熵，KL散度）

相对熵和前面的几个概念联系不大。互熵D(q||p)实际上就是在衡量我们通过计算得出的真实分布的表达式q，究竟与由样本统计得来的分布p有多接近，在衡量多接近这个概念时，我们运用到了熵的形式。PQ完全相同，互熵就等于0了。

其中P代表真实分布，Q代表模型分布。也可写为：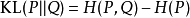

KL散度大于等于0.

其值等于真实分布与拟合分布的交叉熵与真实分布的信息熵之差。
此时是两个分布间的运算，与前面同个分布两个变量的运算不是一个概念。

交叉熵

P的熵是-Σp(x)log(p(x))，Q的熵是-ΣQ(x)log(Q(x))
交叉熵即为-ΣP(x)log(Q(x))
交叉熵是不满足交换律的。
如果说对于第二个例子，仍然使用第一个例子中的策略，如下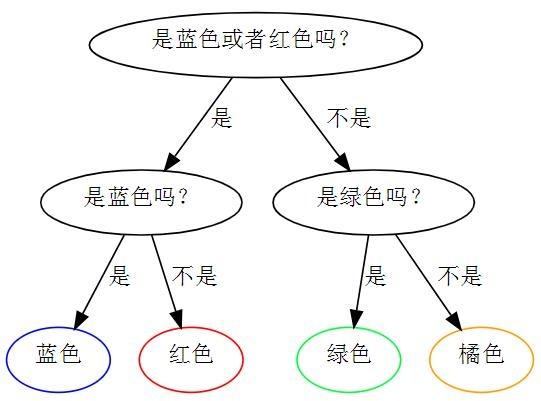

即认为小球分布是(1/4，1/4，1/4，1/4），这个分布就是非真实分布。平均来说, 需要的问题数是 1/8×2+1/8×2+1/4×2+1/2×2=2。 因此, 在例子二中使用例子一的策略是一个比较差的策略. 其中2是这个方案中的交叉熵。而最优方案的交叉熵是1.75。那样预测模型与真实最佳模型是一样的。

即为给定一个策略（分布）, 交叉熵就是在该策略（分布）下猜中颜色所需要的问题的期望值。更普遍的说，交叉熵用来衡量在给定的真实分布下，使用非真实分布所指定的策略产生的熵。

为什么使用交叉熵损失函数

由于KL散度是衡量真实与模型分布的准则，后一项为常数值，KL值大于等于0，所以损失函数为交叉熵即可，使交叉熵越小越好。交叉熵的最小值即为真实分布的熵。