概述
在“无监督学习”( unsupervised learning)中,训练样本的标记信息是未知的,目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础.此类学习任务中研究最多、应用最广的是“聚类”( clustering)
聚类试图将数据集中的样本划分为若干个通常是不相交的子集,每个子集称为一个“簇”(cluster).通过这样的划分,每个簇可能对应于一些潜在的概念(类别),如“浅色瓜”“深色瓜” ,“有籽瓜”,“无籽瓜”,甚至“本地瓜”,“外地瓜”等;需说明的是,这些概念对聚类算法而言事先是未知的,聚类过程仅能自动形成簇结构,簇所对应的概念语义需由使用者来把握和命名.对聚类算法而言,标记簇亦称为类。
聚类既能作为一个单独过程,用于找寻数据内在的分布结构,也可作为分类等其他学习任务的前驱过程.例如,在一些商业应用中需对新用户的类型进行判别,但定义“用户类型”对商家来说却可能不太容易,此时往往可先对用户数据进行聚类,根据聚类结果将每个簇定义为一个类,然后再基于这些类训练分类模型,用于判别新用户的类型.
性能度量
对聚类结果,我们需通过某种性能度量来评估其好坏;另一方面,若明确了最终将要使用的性能度量,则可直接将其作为聚类过程的优化目标,从而更好地得到符合要求的聚类结果.
什么样的聚类结果比较好呢?直观上看,我们希望“物以类聚” ’,即同簇的样本尽可能彼此相似,不同簇的样本尽可能不同.换言之,聚类结果的“簇内相似度”(intra-cluster similarity)高且“簇间相似度”(inter-cluster similarity)低.
聚类性能度量大致有两类一 类是将聚类结果与某个“参考模型”(reference model)进行比较,称为“外部指标”(external index); 另一类是直接考察聚类结果而不利用任何参考模型,称为“内部指标”(internal index).
外部指标

Jaccard系数(Jaccard Coefficient, 简称JC)
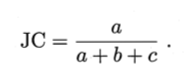
FM指数(Fowlkes and Mallows Index,简称FMI)
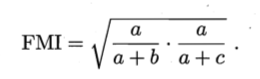
Rand指数(Rand Index,简称RI)
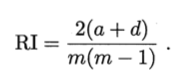
上述性能度量的结果值均在[0, 1]区间,值越大越好。
内部指标
距离越大则样本的相似度越低。
DB指数(Davies- Bouldin Index,简称DBI)
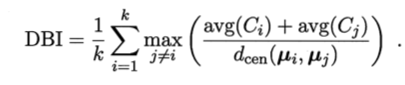
Dunn指数(Dunn Index,简称DI)
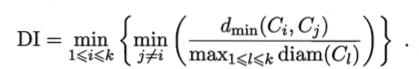
DBI的值越小越好,而DI则相反,值越大越好。
距离计算
对函数dist(,),若它是一个“距离度量”(distance measure),则需满足一些基本性质: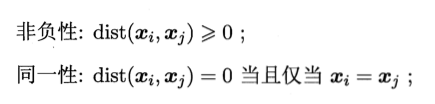
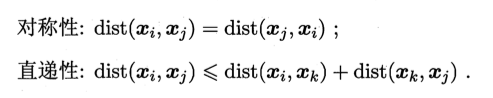
直递性常被直接称为“三角不等式”。
给定样本xi = (xi1;xi2;…;xin) 与xj = (xj1;xj2;..;xjn), 最常用的是“闵可夫斯基距离”(Minkowski distance)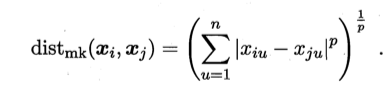
上式即为xi-xj的Lp范数。
当p=2时,闵可夫斯基距离即欧氏距离。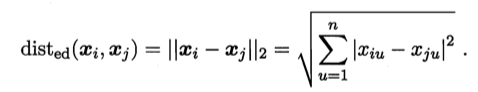
当p=1时,闵可夫斯基距离即曼哈顿距离。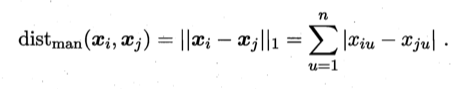
闵可夫斯基距离适用于{1,2,3}这样的有序属性,而不适用于{飞机,火车,轮船}这样的无序属性。对无序属性可采用VDM。

当样本空间中不同属性的重要性不同时,还可使用“加权距离“
通常我们是基于某种形式的距离来定义“相似度度量”(similarity measure), 距离越大,相似度越小.然而,用于相似度度量的距离未必一定要满足距离度量的所有基本性质,尤其是直递性。
原型聚类
k均值算法

最小化式(9.24)并不容易,找到它的最优解需考察样本集D所有可能的簇划分,这是一个NP难问题.因此, k均值算法采用了贪心策略,通过迭代优化来近似求解式(9.24).
对于以下数据集,为方便叙述,将编号为i的样本称为xi,这是一个包含密度与含糖率两个属性值的二维向量。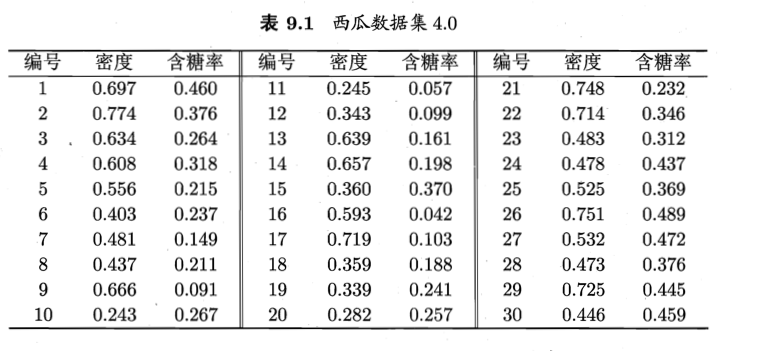

为避免运行时间过长,通常设置一一个最大运行轮数或最小调整幅度阈值,若达到最大轮数或调整幅度小于阈值,则停止运行。
假定聚类簇数k= 3,算法开始时随机选取三个样本x6, x12, x27作为初始均值向量,即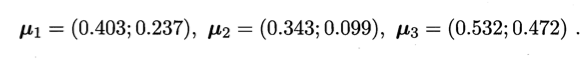
考察样本x1 = (0.697; 0.460),它与当前均值向量μ1, μu2, μ3的距离分别为0.369, 0.506, 0.166, 因此x1将被划入簇C3中.类似的,对数据集中的所有样本
考察一遍后, 可得当前簇划分为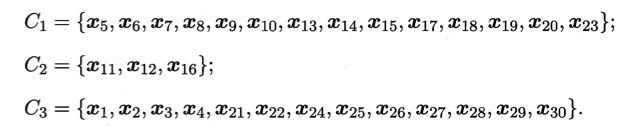
于是,可从C1、C2、C3分别求出新的均值向量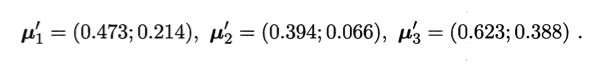
更新当前均值向量后,不断重复上述过程,如图9.3所示,第五轮迭代产生的结
果与第四轮迭代相同,于是算法停止得到最终的簇划分.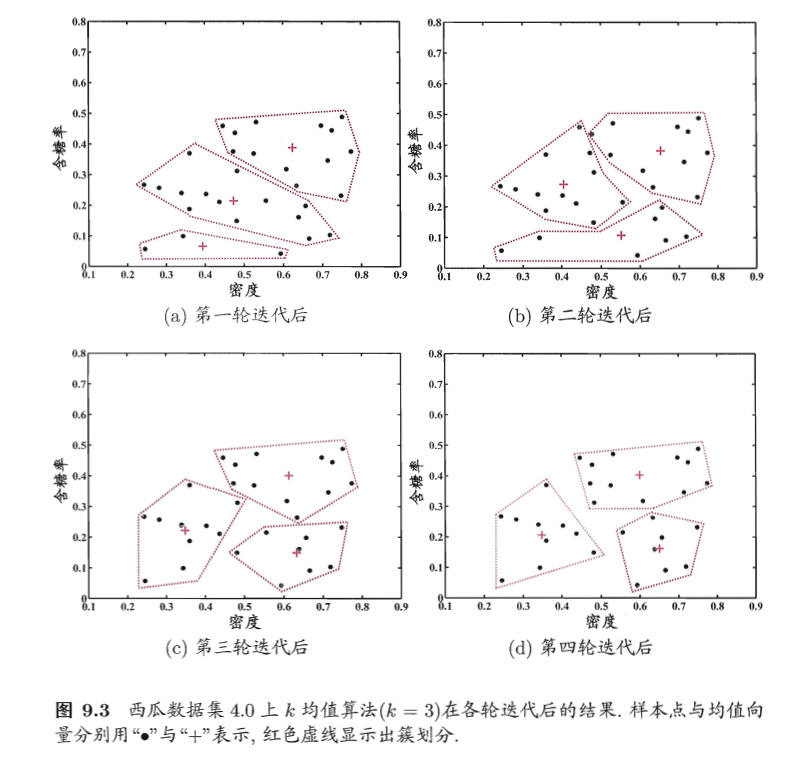
学习向量量化
与k均值算法类似,“ 学习向量量化”(Learning Vector Quantization,简称LVQ)也是试图找到一组原型向量来刻画聚类结构,但与一般聚类算法不同的是,LVQ假设数据样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类.
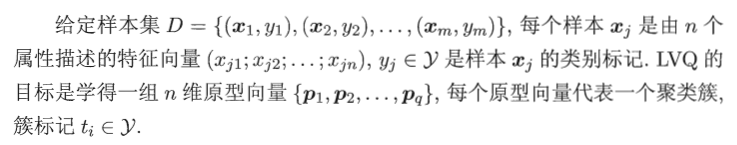

在每一轮迭代中,算法随机选取一个有标记的训练样本,找出与其距离最近的原型向量,并根据两者的类别标记是否一致来对原型向量进行响应的更新。若算法的停止条件已满足,例如已达到最大迭代轮数,或原型向量更新很小甚至不再更新,则将当前原型向量作为最终结果返回。
以西瓜数据集为例演示LVQ的学习过程。假定q=5,即学习目标是找到5个原型向量p1,p2,p3,p4,p5,并假定其对应的类别标记分别为c1,c2,c2,c1,c1。
算法开始时,根据样本的类别标记和簇的预设类别标记对原型向量进行随机初始化,假定初始化为样本x5, x12, x18, x23, x29.在第一轮迭代中,假定随机选取的样本为x1,该样本与当前原型向量p1,p2,p3,p4,p5的距离分别为0.283, 0.506, 0.434, 0.260, 0.032.由于p5与x1距离最近且两者具有相同的类别标记c2,假定学习率η= 0.1,则LVQ更新p5得到新原型向量
高斯混合聚类
与k均值、LVQ用原型向量来刻画聚类结构不同,高斯混合(Mixture-of-Gaussian)聚类采用概率模型来表达聚类原型.
可定义高斯混合分布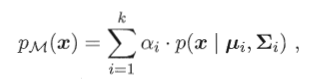

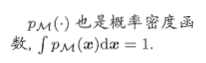
按下不表
密度聚类
密度聚类亦称“基于密度的聚类”(density-based clustering), 此类算法假设聚类结构能通过样本分布的紧密程度确定.通常情形下,密度聚类算法从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇以获得最终的聚类结果.

密度直达关系通常不满足对称性,密度可达关系满足直递性,但不满足对称性.密度相连关系满足对称性。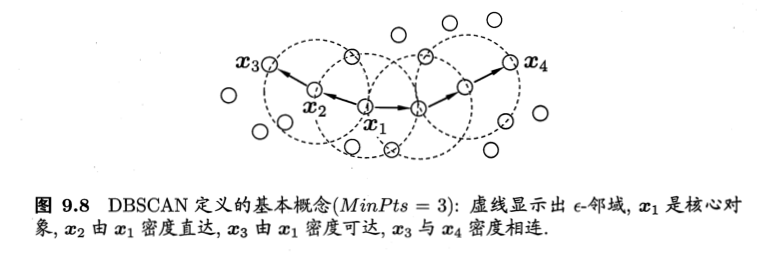

D中不属于任何簇的样本被认为是噪声(noise)或异常(anomaly)样本。
若x为核心对象,由x密度可达的所有样本组成的集合记为X = {x’∈D |x’由x密度可达},则不难证明X即为满足连接性与最大性的簇.
DBSCAN算法先任选数据集中的一个核心对象为“种子”(seed),再由此出发确定相应的聚类簇,算法先根据给定的邻域参数找到所有核心对象;然后以任一核心对象为出发点,找到由其密度可达的样本生成聚类簇,直到所有核心对象均被访问过为止。
以西瓜数据集为例,假定邻域参数设置为e=0.11,MinPts=5.DBSCAN算法先找出各样本的∈-邻域并确定核心对象集合: S= {x3, x5, x6, x8, x9, x13, x14, x18, x19, x24, x25, x28, x29}.然后,从Ω中随机选取一个核心对象作为种子,找出由它密度可达的所有样本,这就构成了第一个聚类簇.不失一般性,假定核心对象x8被选中作为种子,则DBSCAN生成的第一个聚类簇为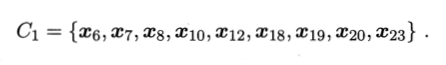
然后, DBSCAN将C1中包含的核心对象从几中去除:Ω=Ω \ C1 ={x3, x5, x9, x13, x14, x24, x25, x28, x2g}.再从更新后的集合8中随机选取一个核心对象作为种子来生成下一一个聚类簇..上述过程不断重复,直至I为空.图9.10显示DBSCAN先后生成聚类簇的情况. C1之后生成的聚类簇为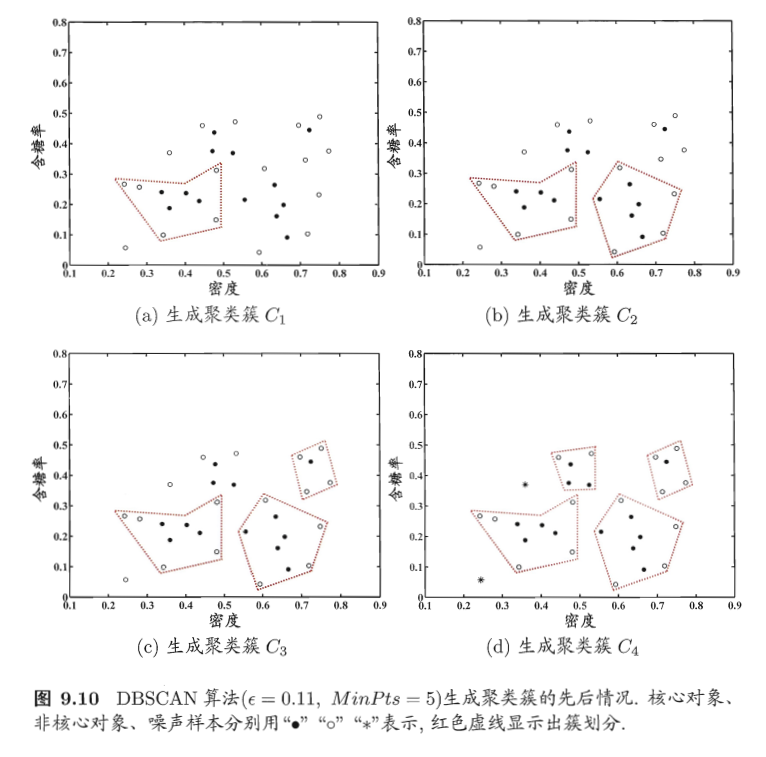

层次聚类
层次聚类(hierarchical clustering)试图在不同层次对数据集进行划分,从而形成树形的聚类结构.数据集的划分可采用“自底向上”的聚合策略,也可采用“自顶向下”的分拆策略.
AGNES是一种采用自底向上聚合策略的层次聚类算法.它先将数据集中的每个样本看作一个初始聚类簇,然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复,直至达到预设的聚类簇个数.这里的关键是如何计算聚类簇之间的距离.实际上,每个簇是一个样本集合,因此,只需采用关于集合的某种距离即可。
对于给定聚类簇Ci,Cj,可通过下面式子来计算距离: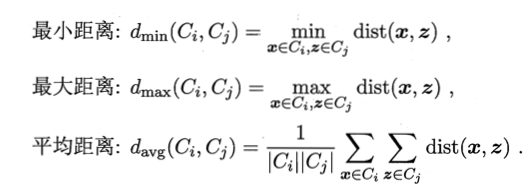
显然,最小距离由两个簇的最近样本决定,最大距离由两个簇的最远样本决定,而平均距离则由两个簇的所有样本共同决定.当聚类簇距离由dmin,dmax或davg计算时,AGNES算法被相应地称为“单链接”(single-linkage)、 “ 全链接”(complete linkage)或“均链接”(average-linkage)算法.
AGNES算法先对仅含一个样本的初始聚类簇和相应的距离矩阵进行初始化;然后AGNES不断合并距离最近的聚类簇,并对合并得到的聚类簇的距离矩阵进行更新;上述过程不断重复,直至达到预设的聚类簇数.