博客

RNN是在自然语言处理领域中最先被用起来的，使用RNN之前，语言模型主要是采用N-Gram。N可以是一个自然数，比如2或者3。它的含义是，假设一个词出现的概率只与前面N个词相关。

如果用2-Gram进行建模，那么电脑在预测的时候，只会看到前面的『了』，然后，电脑会在语料库中，搜索『了』后面最可能的一个词。不管最后电脑选的是不是『我』，我们都知道这个模型是不靠谱的，因为『了』前面说了那么一大堆实际上是没有用到的。如果是3-Gram模型呢，会搜索『批评了』后面最可能的词，感觉上比2-Gram靠谱了不少，但还是远远不够的。因为这句话最关键的信息『我』，远在9个词之前！

读者可能会想，可以提升继续提升N的值呀，比如4-Gram、5-Gram…….。实际上，这个想法是没有实用性的。因为我们想处理任意长度的句子，N设为多少都不合适；另外，模型的大小和N的关系是指数级的，4-Gram模型就会占用海量的存储空间。

所以，该轮到RNN出场了，RNN理论上可以往前看(往后看)任意多个词。

基本循环神经网络

下图是一个简单的循环神经网络如，它由输入层、一个隐藏层和一个输出层组成：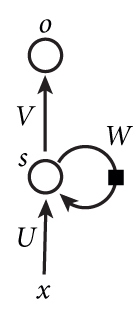

循环神经网络实在是太难画出来了，网上所有大神们都不得不用了这种抽象艺术手法。如果把上面有W的那个带箭头的圈去掉，它就变成了最普通的全连接神经网络。x是一个向量，它表示输入层的值（这里面没有画出来表示神经元节点的圆圈）；s是一个向量，它表示隐藏层的值（这里隐藏层面画了一个节点，你也可以想象这一层其实是多个节点，节点数与向量s的维度相同）；U是输入层到隐藏层的权重矩阵。o也是一个向量，它表示输出层的值；V是隐藏层到输出层的权重矩阵。循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x，还取决于上一次隐藏层的值s。权重矩阵 W就是隐藏层上一次的值作为这一次的输入的权重。

把上面的图展开，循环神经网络也可以画成下面这个样子：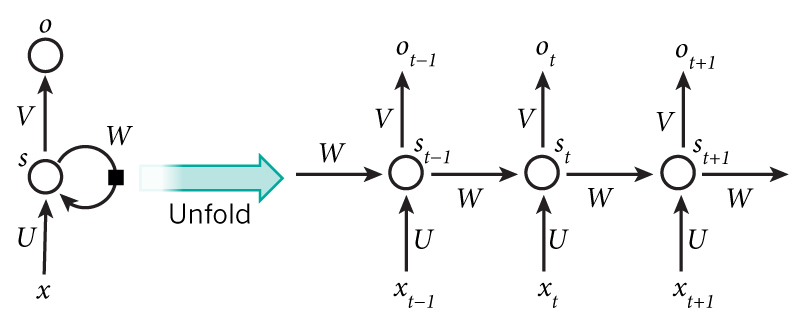

现在看上去就比较清楚了，这个网络在t时刻接收到输入x𝑡之后，隐藏层的值是s𝑡，输出值是o𝑡。关键一点是，s𝑡的值不仅仅取决于x𝑡，还取决于s𝑡−1。我们可以用下面的公式来表示循环神经网络的计算方法：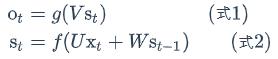

式1是输出层的计算公式，输出层是一个全连接层，也就是它的每个节点都和隐藏层的每个节点相连。V是输出层的权重矩阵，g是激活函数。式2是隐藏层的计算公式，它是循环层。U是输入x的权重矩阵，W是上一次的值s𝑡−1作为这一次的输入的权重矩阵，f是激活函数。

如果反复把式2带入到式1，我们将得到：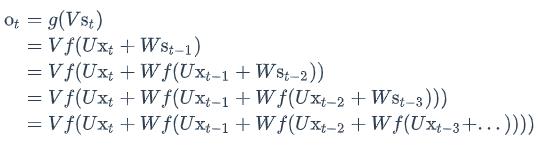

从上面可以看出，循环神经网络的输出值𝑜𝑡，是受前面历次输入值x𝑡、x𝑡−1、x𝑡−2、x𝑡−3…影响的，这就是为什么循环神经网络可以往前看任意多个输入值的原因。

双向循环神经网络

对于语言模型来说，很多时候光看前面的词是不够的，比如下面这句话：

我们需要双向循环神经网络，如下图所示：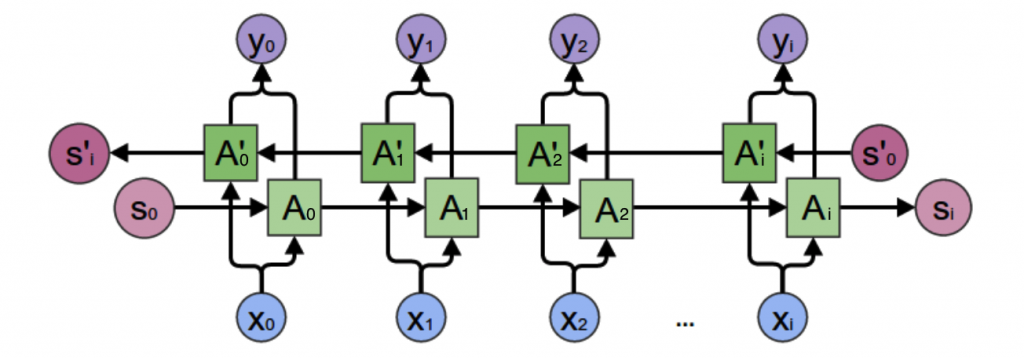

从上图可以看出，双向卷积神经网络的隐藏层要保存两个值，一个A参与正向计算，另一个值A’参与反向计算。最终的输出值y2取决于𝐴2和𝐴′2。其计算方法为：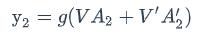

𝐴2 和𝐴′2则分别计算：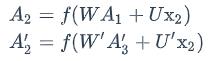

现在，我们已经可以看出一般的规律：正向计算时，隐藏层的值s𝑡与s𝑡−1有关；反向计算时，隐藏层的值s′𝑡与s′𝑡+1有关；最终的输出取决于正向和反向计算的加和。现在，我们仿照式1和式2，写出双向循环神经网络的计算方法：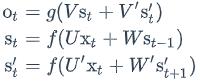

从上面三个公式我们可以看到，正向计算和反向计算不共享权重，也就是说U和U’、W和W’、V和V’都是不同的权重矩阵。

深度循环神经网络

前面我们介绍的循环神经网络只有一个隐藏层，我们当然也可以堆叠两个以上的隐藏层，这样就得到了深度循环神经网络。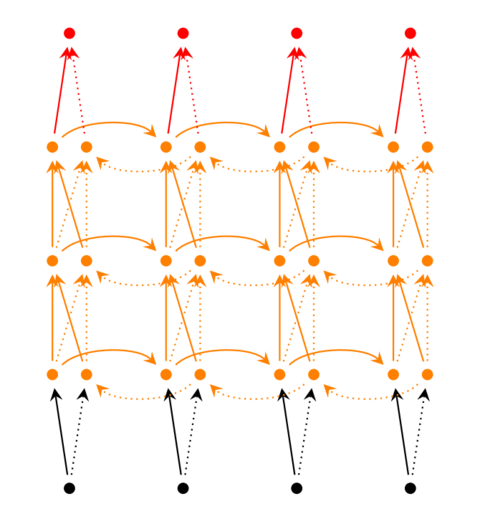

我们把第i个隐藏层的值表示为s(𝑖)𝑡和s′(𝑖)𝑡，则深度循环神经网络的计算方式可以表示为：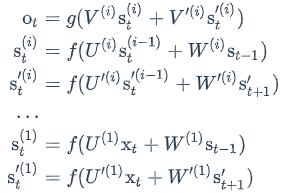

循环神经网络的训练

循环神经网络的训练算法：BPTT
BPTT算法是针对循环层的训练算法，它的基本原理和BP算法是一样的，也包含同样的三个步骤：

前向计算每个神经元的输出值
反向计算每个神经元的误差项𝛿𝑗值，它是误差函数E对神经元j的加权输入𝑛𝑒𝑡𝑗的偏导数；
计算每个权重的梯度。

最后再用随机梯度下降算法更新权重。

循环层如下图所示：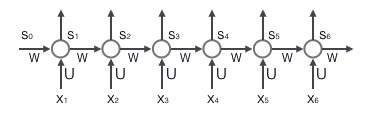

前向计算：
使用前面的式2对循环层进行前向计算：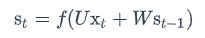

注意，上面的s𝑡、x𝑡、s𝑡−1都是向量，用黑体字母表示；而U、V是矩阵，用大写字母表示。向量的下标表示时刻，例如，s𝑡表示在t时刻向量s的值。

我们假设输入向量x的维度是m，输出向量s的维度是n，则矩阵U的维度是n m，矩阵W的维度是n m。下面是上式展开成矩阵的样子，看起来更直观一些：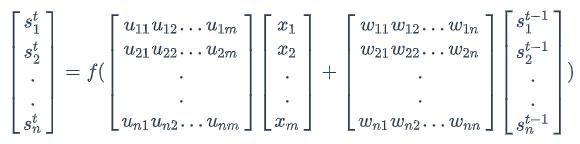

在这里我们用手写体字母表示向量的一个元素，它的下标表示它是这个向量的第几个元素，它的上标表示第几个时刻。例如，𝑠𝑡𝑗表示向量s的第j个元素在t时刻的值。𝑢𝑗𝑖表示输入层第i个神经元到循环层第j个神经元的权重。𝑤𝑗𝑖表示循环层第t-1时刻的第i个神经元到循环层第t个时刻的第j个神经元的权重。

误差项的计算
BTPP算法将第l层t时刻的误差项𝛿𝑙𝑡值沿两个方向传播，一个方向是其传递到上一层网络，得到𝛿𝑙−1𝑡，这部分只和权重矩阵U有关；另一个是方向是将其沿时间线传递到初始𝑡1时刻，得到𝛿𝑙1，这部分只和权重矩阵W有关。

我们用向量net𝑡表示神经元在t时刻的加权输入，因为：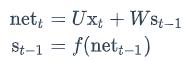

因此：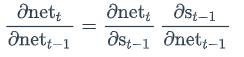

我们用a表示列向量，用a𝑇表示行向量。上式的第一项是向量函数对向量求导，其结果为Jacobian矩阵：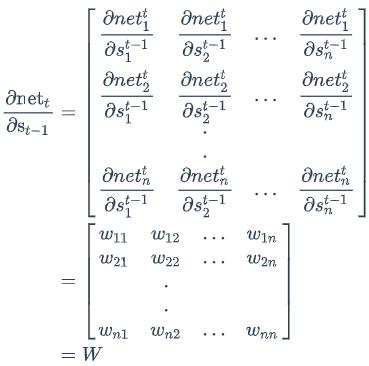

同理，上式第二项也是一个Jacobian矩阵：

其中，diag[a]表示根据向量a创建一个对角矩阵，即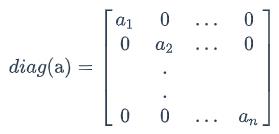

最后，将两项合在一起，可得：

上式描述了将𝛿沿时间往前传递一个时刻的规律，有了这个规律，我们就可以求得任意时刻k的误差项𝛿𝑘：

式3就是将误差项沿时间反向传播的算法。循环层将误差项反向传递到上一层网络，与普通的全连接层是完全一样的。
循环层的加权输入net𝑙与上一层的加权输入net𝑙−1关系如下：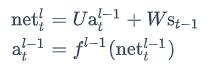

上式中net𝑙𝑡是第l层神经元的加权输入(假设第l层是循环层)；net𝑙−1𝑡是第l-1层神经元的加权输入；a𝑙−1𝑡是第l-1层神经元的输出；𝑓𝑙−1是第l-1层的激活函数。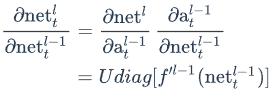

所以，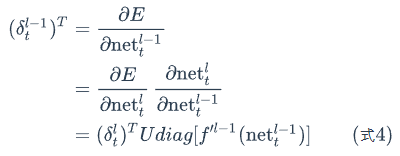

式4就是将误差项传递到上一层算法。

权重梯度的计算
现在，我们终于来到了BPTT算法的最后一步：计算每个权重的梯度。

首先，我们计算误差函数E对权重矩阵W的梯度∂𝐸 / ∂𝑊。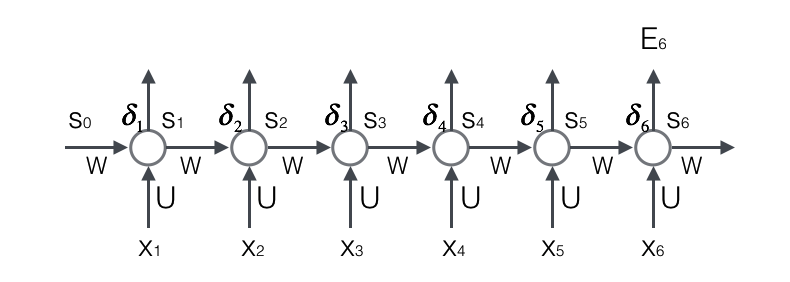

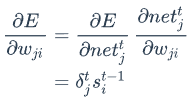
具体推导参考
https://cuijiahua.com/blog/2018/12/dl-11.html

RNN的梯度爆炸和消失问题

不幸的是，实践中前面介绍的几种RNNs并不能很好的处理较长的序列。一个主要的原因是，RNN在训练中很容易发生梯度爆炸和梯度消失，这导致训练时梯度不能在较长序列中一直传递下去，从而使RNN无法捕捉到长距离的影响。

为什么RNN会产生梯度爆炸和消失问题呢？我们接下来将详细分析一下原因。我们根据式3可得：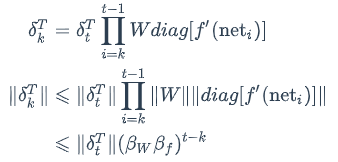

上式的𝛽定义为矩阵的模的上界。因为上式是一个指数函数，如果t-k很大的话（也就是向前看很远的时候），会导致对应的误差项的值增长或缩小的非常快，这样就会导致相应的梯度爆炸和梯度消失问题（取决于𝛽大于1还是小于1）。

通常来说，梯度爆炸更容易处理一些。因为梯度爆炸的时候，我们的程序会收到NaN错误。我们也可以设置一个梯度阈值，当梯度超过这个阈值的时候可以直接截取。

梯度消失更难检测，而且也更难处理一些。总的来说，我们有三种方法应对梯度消失问题：

合理的初始化权重值。初始化权重，使每个神经元尽可能不要取极大或极小值，以躲开梯度消失的区域。
使用relu代替sigmoid和tanh作为激活函数。
使用其他结构的RNNs，比如长短时记忆网络（LTSM）和Gated Recurrent Unit（GRU），这是最流行的做法。

向量化

我们知道，神经网络的输入和输出都是向量，为了让语言模型能够被神经网络处理，我们必须把词表达为向量的形式，这样神经网络才能处理它。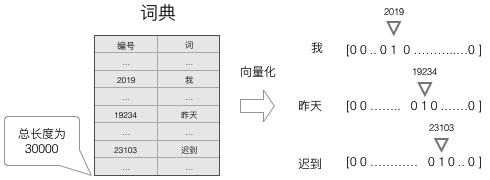

使用这种向量化方法，我们就得到了一个高维、稀疏的向量（稀疏是指绝大部分元素的值都是0）。处理这样的向量会导致我们的神经网络有很多的参数，带来庞大的计算量。因此，往往会需要使用一些降维方法，将高维的稀疏向量转变为低维的稠密向量。

语言模型要求的输出是下一个最可能的词，我们可以让循环神经网络计算计算词典中每个词是下一个词的概率，这样，概率最大的词就是下一个最可能的词。因此，神经网络的输出向量也是一个N维向量，向量中的每个元素对应着词典中相应的词是下一个词的概率。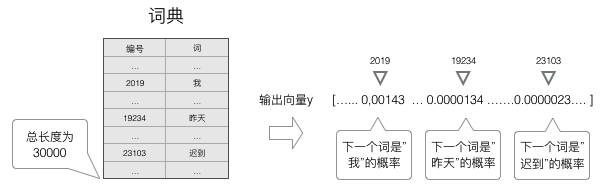

Softmax层

语言模型是对下一个词出现的概率进行建模。那么，怎样让神经网络输出概率呢？方法就是用softmax层作为神经网络的输出层。

softmax函数的定义：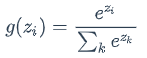

举一个例子。Softmax层如下图所示：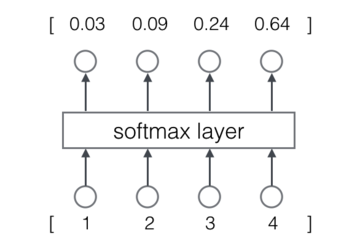

计算过程为：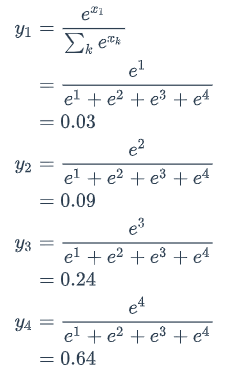

输出向量y的特征：

每一项为取值为0-1之间的正数；
所有项的总和是1。

这些特征和概率的特征是一样的，因此我们可以把它们看做是概率。对于语言模型来说，我们可以认为模型预测下一个词是词典中第一个词的概率是0.03，是词典中第二个词的概率是0.09，以此类推。

交叉熵误差
一般来说，当神经网络的输出层是softmax层时，对应的误差函数E通常选择交叉熵误差函数，其定义如下：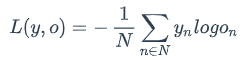

在上式中，N是训练样本的个数，向量𝑦𝑛是样本的标记，向量𝑜𝑛是网络的输出。标记𝑦𝑛是一个one-hot向量，例如𝑦1=[1,0,0,0]，如果网络的输出𝑜=[0.03,0.09,0.24,0.64]，那么，交叉熵误差是（假设只有一个训练样本，即N=1）：

我们当然可以选择其他函数作为我们的误差函数，比如最小平方误差函数(MSE)。不过对概率进行建模时，选择交叉熵误差函数更make sense。具体原因，
https://jamesmccaffrey.wordpress.com/2011/12/17/neural-network-classification-categorical-data-softmax-activation-and-cross-entropy-error/