博客
参考深度学习实战教程(四):卷积神经网络
卷积神经网络常见架构,也就是N个卷积层叠加,然后(可选)叠加一个Pooling层,重复这个结构M次,最后叠加K个全连接层。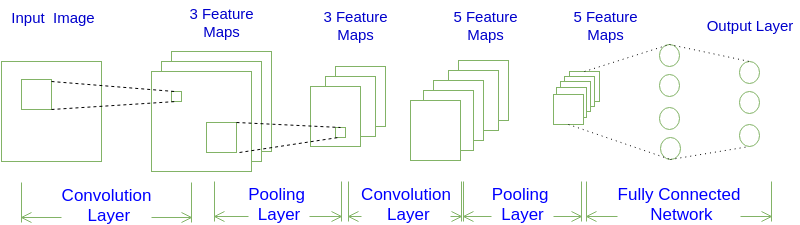
卷积神经网络的层结构和全连接神经网络的层结构有很大不同。全连接神经网络每层的神经元是按照一维排列的,也就是排成一条线的样子;而卷积神经网络每层的神经元是按照三维排列的,也就是排成一个长方体的样子,有宽度、高度和深度。
对于上图展示的神经网络,输入层的宽度和高度对应于输入图像的宽度和高度,而它的深度为1。接着,第一个卷积层对这幅图像进行了卷积操作,得到了三个Feature Map。因为图中看出这个卷积层包含三个Filter,也就是三套参数,每个Filter都可以把原始输入图像卷积得到一个Feature Map,三个Filter就可以得到三个Feature Map。至于一个卷积层可以有多少个Filter,那是可以自由设定的。也就是说,卷积层的Filter个数也是一个超参数。我们可以把Feature Map可以看做是通过卷积变换提取到的图像特征,三个Filter就对原始图像提取出三组不同的特征,也就是得到了三个Feature Map,也称做三个通道(channel)。
在第一个卷积层之后,Pooling层对三个Feature Map做了下采样,得到了三个更小的Feature Map。接着,是第二个卷积层,它有5个Filter。每个Fitler都把前面下采样之后的3个Feature Map卷积在一起,得到一个新的Feature Map。这样,5个Filter就得到了5个Feature Map。接着,是第二个Pooling,继续对5个Feature Map进行下采样,得到了5个更小的Feature Map。
上图最后两层是全连接层,第一个全连接层的每个神经元,和上一层5个Feature Map中的每个神经元相连,第二个全连接层(也就是输出层)的每个神经元,则和第一个全连接层的每个神经元相连,这样得到了整个网络的输出。
对于卷积操作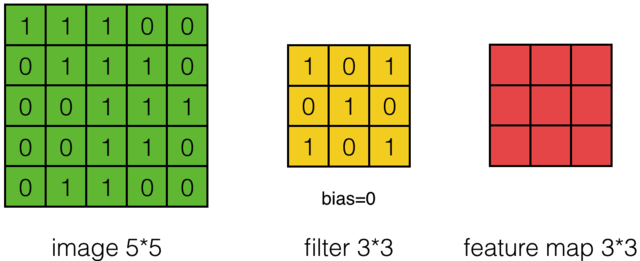
用X𝑖,𝑗表示图像的第i行第j列元素;对filter的每个权重进行编号,用W𝑚,𝑛表示第m行第n列权重,用𝑤𝑏表示filter的偏置项;对Feature Map的每个元素进行编号,用𝑎𝑖,𝑗表示Feature Map的第i行第j列元素;用f表示激活函数(这个例子选择relu函数作为激活函数)。然后,使用下列公式计算卷积: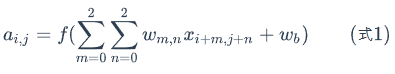
在卷积过程中,可以设置步幅strid。
图像大小、步幅和卷积后的Feature Map大小有关。
在上面两个公式中,𝑊2是卷积后Feature Map的宽度;𝑊1是卷积前图像的宽度;𝐹是filter的宽度;𝑃是Zero Padding数量,Zero Padding是指在原始图像周围补几圈0,如果𝑃的值是1,那么就补1圈0;𝑆是步幅;𝐻2是卷积后Feature Map的高度;𝐻1是卷积前图像的宽度。式2和式3本质上是一样的。
如果卷积前的图像深度为D,那么相应的filter的深度也必须为D。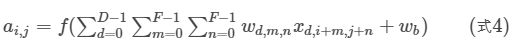
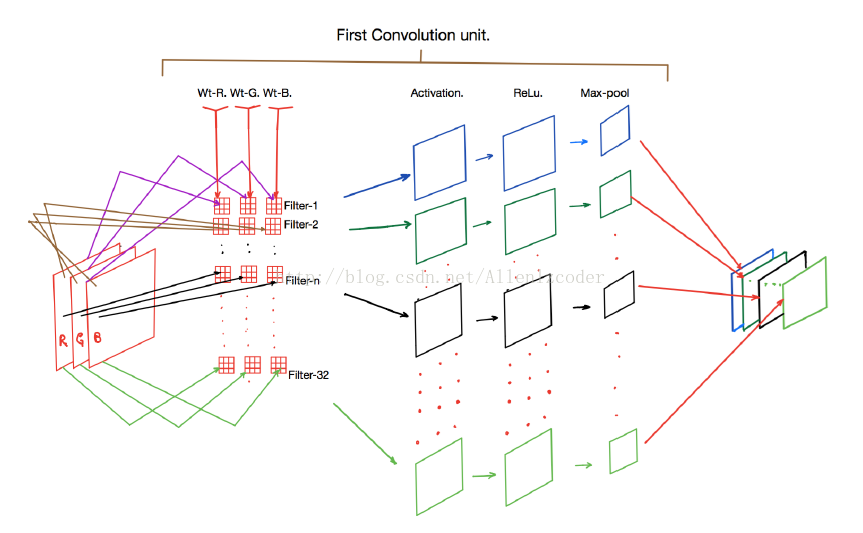
我们前面还曾提到,每个卷积层可以有多个filter。每个filter和原始图像进行卷积后,都可以得到一个Feature Map。因此,卷积后Feature Map的个数和卷积层的filter个数是相同的。
这里面体现了局部连接和权值共享:每层神经元只和上一层部分神经元相连(卷积计算规则),且filter的权值对于上一层所有神经元都是一样的。对于包含两个3* 3 *3的fitler的卷积层来说,其参数数量仅有(3 * 3 * 3+1) * 2=56个,且参数数量与上一层神经元个数无关。与全连接神经网络相比,其参数数量大大减少了。
池化层的操作
Pooling层主要的作用是下采样,通过去掉Feature Map中不重要的样本,进一步减少参数数量。Max Pooing之外,常用的还有Mean Pooling——取各样本的平均值。对于深度为D的Feature Map,各层独立做Pooling,因此Pooling后的深度仍然为D。
卷积神经网络的训练
和全连接神经网络相比,卷积神经网络的训练要复杂一些。但训练的原理是一样的:利用链式求导计算损失函数对每个权重的偏导数(梯度),然后根据梯度下降公式更新权重。训练算法依然是反向传播算法。
对于卷积神经网络,由于涉及到局部连接、下采样的等操作,影响到了第二步误差项𝛿的具体计算方法,而权值共享影响了第三步权重𝑤的梯度的计算方法。
卷积层的训练
获得了所有的梯度之后,就是根据梯度下降算法来更新每个权重。
Pooling层的训练
无论max pooling还是mean pooling,都没有需要学习的参数。因此,在卷积神经网络的训练中,Pooling层需要做的仅仅是将误差项传递到上一层,而没有梯度的计算。
详见https://cuijiahua.com/blog/2018/12/dl-10.html
美团 卷积神经网络
卷积神经网络中最重要的两个概念是卷积和池化。
卷积操作在信号处理中可以看作滤波过程,过滤或提取出需要的频段信息。相应的,图像处理中也可实现不同功能的卷积操作,如边缘轮廓,锐化,模糊化等。简言之,卷积核沿着输入矩阵从左到右,从上到下遍历,每到一个网格,其输出是输入矩阵对应位置元素相乘并求和。如下图所示的卷积操作过程可以看出,如果卷积核设计得当(可以通过网络学习出来),不同层次的局部重要信息就能提取出来,另一方面卷积核共享参数能显著降低参数量。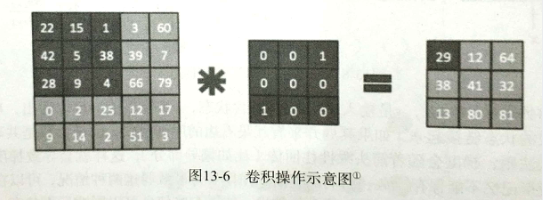
另外一个重要的概念是池化,下图为最大池化的操作。池化有两个作用:一个是降维,另一个就是保持局部不变性,提取抽象信息。深灰色区域在池化后的输出值为6,而且即使该区域的像素发生扰动(像素值不超过6),输出值也不会变,因此具备一定健壮性。
卷积神经网络在计算机视觉应用非常广,包括图像分类,检测,识别等,从2012年的AlexNet,到2014年的VGG,2015年的GoogleNet,2016年的ResNet,都是卷积神经网络不断演化并在ImageNet比赛上不断刷新成绩。卷积神经网络在自然语言处理方向也有很好的应用,比如情感分类,文本匹配等。
百面 深度卷积神经网络
卷积神经网络是一种前馈神经网络,其特点是每层的神经元节点只响应前一层局部区域范围内的神经元(全连接网络中每个神经元节点响应前一层的全部节点)。一个深度卷积神经网络模型通常由若干卷积层叠加若干全连接层组成,中间也包括各种非线性操作以及池化操作。卷积神经网络同样可以使用反向传播算法进行训练,相较于其他网络模型,卷积神经网络的参数共享特性使得需要优化的参数数目大大缩减,提高了模型的训练效率以及可扩展性。由于卷积运算主要用于处理类网格结构的数据,因此对于时间序列以及图像数据的分析与识别具有显著优势。
问题1
问:卷积操作的本质特性包括系数交互和参数共享,具体解释这两种特性及其作用。
答:稀疏交互(sparse interaction)
在传统神经网络中,网络层之间输入与输出的连接关系可以由一个权值参数矩阵来表示,其中每个单独的参数值都表示了前后层某两个神经元节点之间的交互。对于全连接网络,任意一对输入与输出神经元之间都产生交互,形成稠密的连接结构。
而在卷积神经网络中,卷积核尺度远小于输入的维度,这样每个输出神经元仅与前一层特定局部区域内的神经元存在连接权重(即产生交互),我们称这种特性为稀疏交互。具体来说,假设网络中相邻两层分别有m个输入和n个输出,全连接网络中权值参数矩阵将包含m * n个参数。对于稀疏交互的卷积神经网络,如果限定每个输出与前一层神经元的连接数为k,那么该层的参数总量为k * n。在实际应用中,一般k值远小于m就可以取得较为可观的效果;而此时优化过程的时间复杂度将会减小几个数量级,过拟合的情况也得到较好的改善。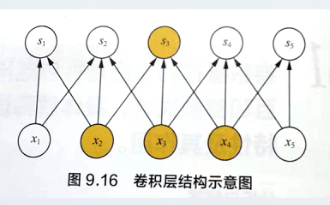
稀疏交互的物理意义是,通常图像,文本,语音等现实世界中的数据都具有局部的特征结构,我们可以先学习局部的特征,再将局部的特征组合起来形成更复杂和抽象的特征。
参数共享(Parameter Sharing)
参数共享是指在同一个模型的不同模块中使用相同的参数,它是卷积运算的固有属性。全连接网络中,计算每层的输出时,权值参数矩阵中的每个元素只作用于某个输入元素一次;而在卷积神经网络中,卷积核中的每一个元素将作用于每一次局部输入的特定位置上。根据参数共享的思想,我们只需要学习一组参数集合,而不需要针对每个位置的每个参数都进行优化,从而大大降低了模型的存储需求。
参数共享的物理意义是使得卷积层具有平移等特性。假如图像中有一只猫,那么无论它出现在图像中的任何位置,我们都应该将它识别为猫,也就是说神经网络的输出对于平移变换来说应当是等变的。特别地,当函数f(x)与g(x)满足f(g(x))=g(f(x))时我们称f(x)关于变换g具有等变性。也就是说,在猫的图片上先进行卷积,再向右平移l像素的输出,与先将图片向右平移l像素再进行卷积操作的输出结果是相等的。
问题3
问:卷积神经网络如何用于文本分类任务?
答:卷积神经网络的核心思想是捕捉局部特征,最初在图像领域取得了巨大的成功,后来在文本领域也得到了广泛的应用。对于文本来说,局部特征就是由若干单词组成的滑动窗口,类似于N-gram特征进行组合和筛选,获得不同抽象层次的语义信息。由于在每次卷积中采用了共享权重的机制,因此它的训练速度相对较快,在实际的文本分类任务中取得了非常不错的效果。
下图是一个用卷积神经网络模型进行文本表示,并最终用于文本分类的网络结构。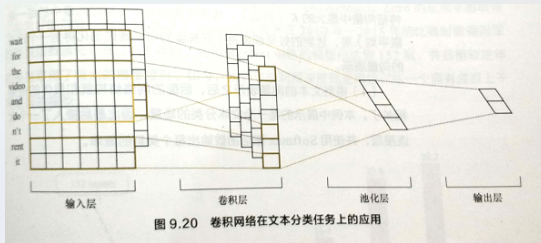
输入层是一个N * K的矩阵,其中N为文章所对应的单词总数,K是每个词对应的表示向量的维度。每个词的K维向量可以是预先在其他语料库中训练好的,也可以作为未知的参数有网络训练得到。这两种方法各有优势,一方面,预先训练的词嵌入可以利用其他语料库得到更多的先验知识;另一方面,由当前网络训练的词向量能够更好地抓住与当前任务相关联的特征。因此,图中的输入层实际采用了两个通道的形式,即有两个N * K的输入矩阵,其中一个用预先训练好的词嵌入表达,并且在训练过程中不再发生变化;另外一个也由同样的方式初始化,但是会作为参数,随着网络的训练发生改变。