百面机器学习
深度前馈网络是一类网络模型的统称,常见的多层感知机,自编码器,限制玻尔兹曼机,以及卷积神经网络等,都是其中的成员。
在人工神经网络领域中,感知机也被认为是单层的人工神经网络。
多层感知机与布尔函数
神经网络概念的诞生很大程度上受到了神经科学的启发。生物学研究表明,大脑皮层的感知与计算功能是分层实现的,例如视觉图像,首先光信号进入大脑皮层的V1区,即初级视皮层,之后依次通过V2层和V4层,即纹外皮层,进入下叶参与物体识别。深度神经网络,除了模拟人脑功能的多层结构,最大的优势在于能够以紧凑简洁的方式来表达比浅层网络更复杂的函数集合(这里的简洁定义为隐层单元的数目与输入单元的数目呈多项式关系)。
问题1
问:多层感知机表示异或逻辑时最少需要几个隐含层(仅考虑二元输入)?
答:回顾逻辑回归的公式Z=sigmoid(AX+BY+C),发现如果用表示XY的异或关系,采用逻辑回归(即不带隐藏层的感知机)无法精确学习出一个输出为异或的模型表示。
考虑有一个隐藏层的情况,通用近似定理表示,一个前馈神经网络如果具有线性输出层和至少一层具有任何一种“挤压”性质的激活函数的隐藏层,当给予网络足够数量的隐藏单元时,可以以任意精度近似任何从一个有限维空间到另一个有限维空间的波莱尔可测函数。可以简单的认为我们常用的激活函数和目标函数是通用近似定理适用的一个子集,因此多层感知机的表达能力是非常强的,关键在于我们是否能够学习到对应此表达的模型参数。
第一个隐藏单元在X和Y均为1时激活,第二个隐藏单元在X和Y均为0时激活,最后再将两个隐藏单元的输出做一个线性变换即可事先异或操作。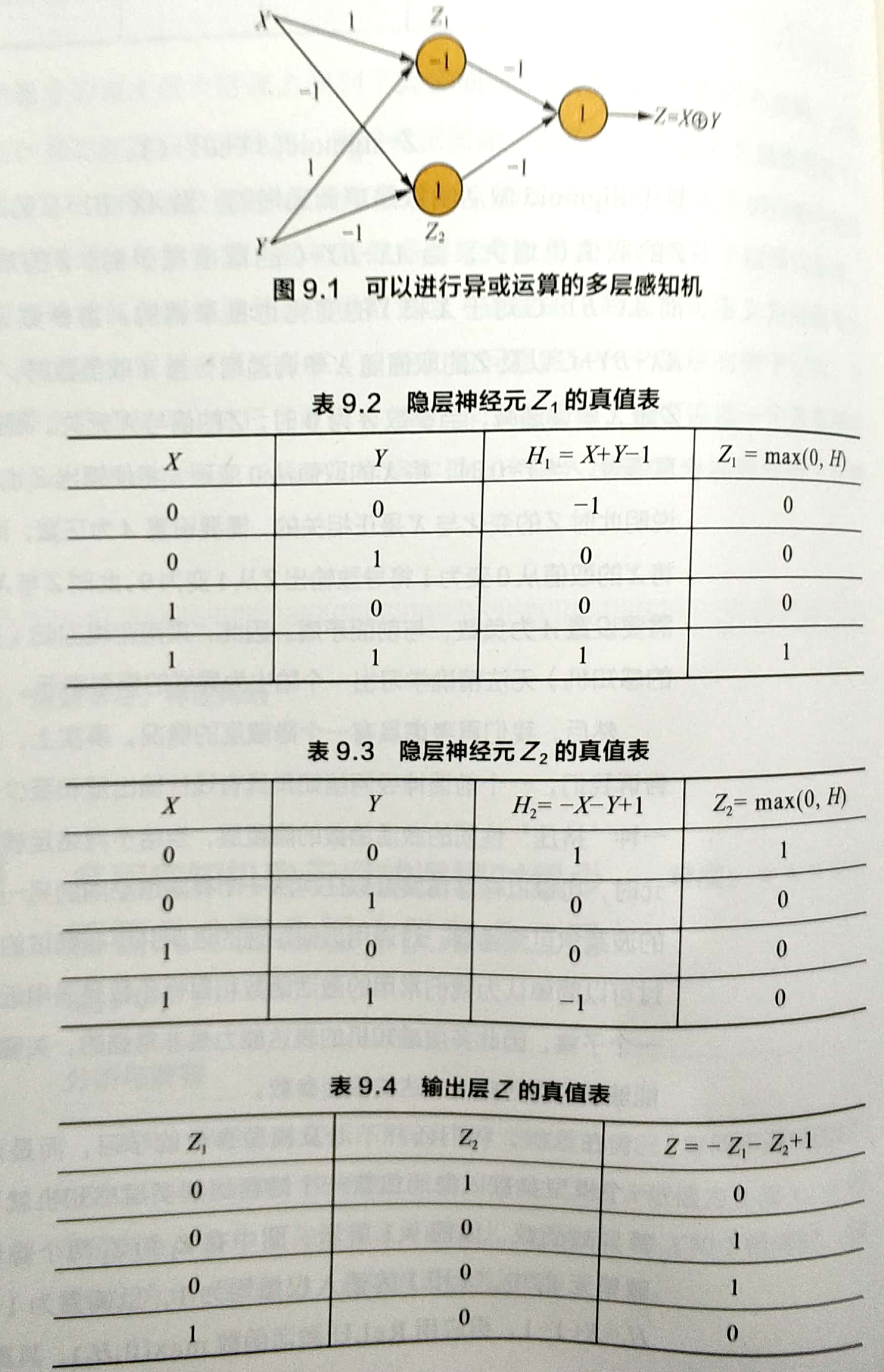
问题2
问:如果只使用一个隐层,需要多少隐节点能够实现包含n元输入的任意布尔函数?
答:包含n元输入的任意布尔函数可以唯一表示为析取范式,当n=5时的简单范例: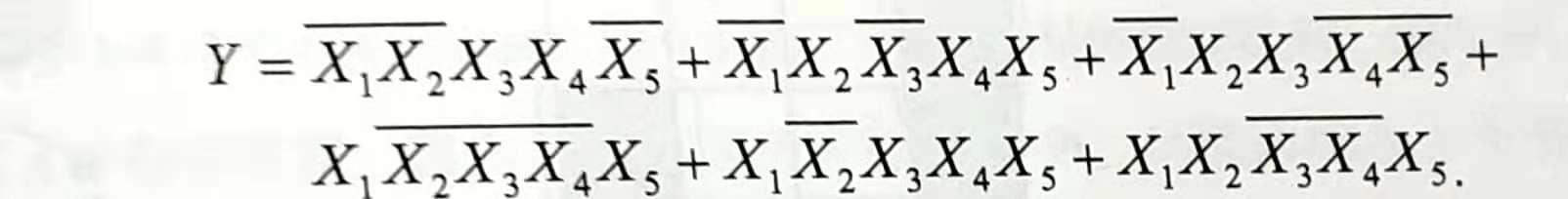
最终的输出Y可以表示成由6个合取范式所组成的析取范式。该函数可由包含6个隐节点的3层感知机实现。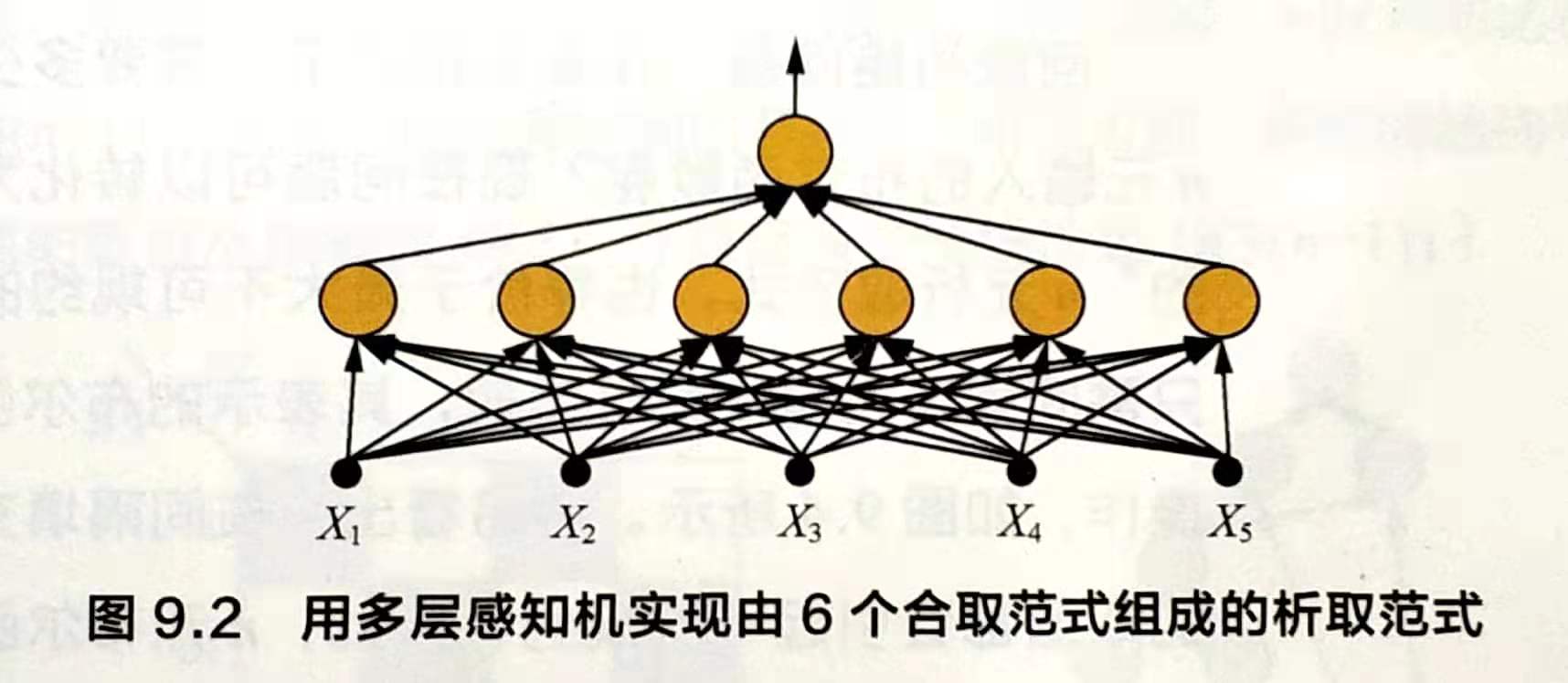
首先证明单个隐节点可以表示任意合取范式。考虑任意布尔变量假设Xi,若它在合取范式中出现的形式为正(Xi),则设权重为1;若出现的形式为非,则设置权重为-1;若没有在合取范式中出现。设置权重为0;并且偏置设为合取范式中变量的总数取负加1。可以看出,当采用ReLU激活函数之后,当且仅当所有出现的布尔变量均满足条件时,该隐藏单元才会被激活(输出1),否则输出0,这与合取范式的定义的相符。然后,令所有隐藏单元到输出层的参数为1,并设输出单元的偏置为0.这样,当且仅当所有的隐藏单元到输出层的参数为1,并设输出单元的偏置为0.这样,当且仅当所有的隐藏单元都未被激活时才会输出0,否则都将输出一个正数,起到了析取的作用。
可以使用卡诺图表示析取式,即用网格表示真值表,当输入的合取式值为1时,则填充相应的网格。卡诺图中相邻的填色区域可以进行规约,以达到化简布尔函数的目的。该函数可由包含3个隐节点的3层感知机实现: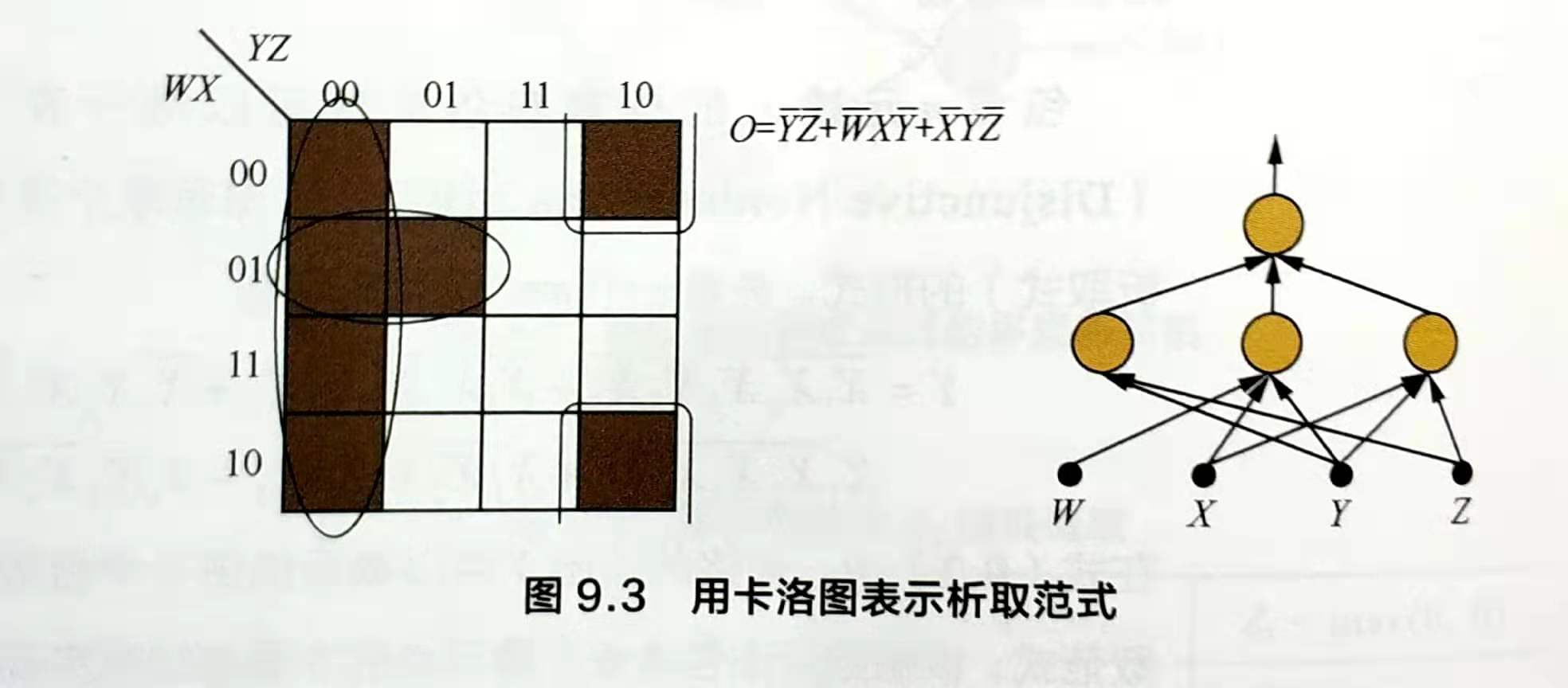
回顾初始的问题:在最差的情况下,需要多少个隐藏结点来表示包含n元输入的布尔函数呢?现在问题可以转化为:寻找“最大不可规约的”n元析取范式,也等价于最大不可规约的卡诺图。直观上,我们只需间隔填充网格即可实现,其表示的布尔函数恰为n元输入的异或操作,如下图,容易看出,在间隔填充的网格上反转任意网格的取值都会引起一次规约,因此,n元布尔函数的析取范式最多包含2^(n-1)个不可规约的合取范式,对于单隐层的感知机,需要2^(n-1)个隐节点来实现。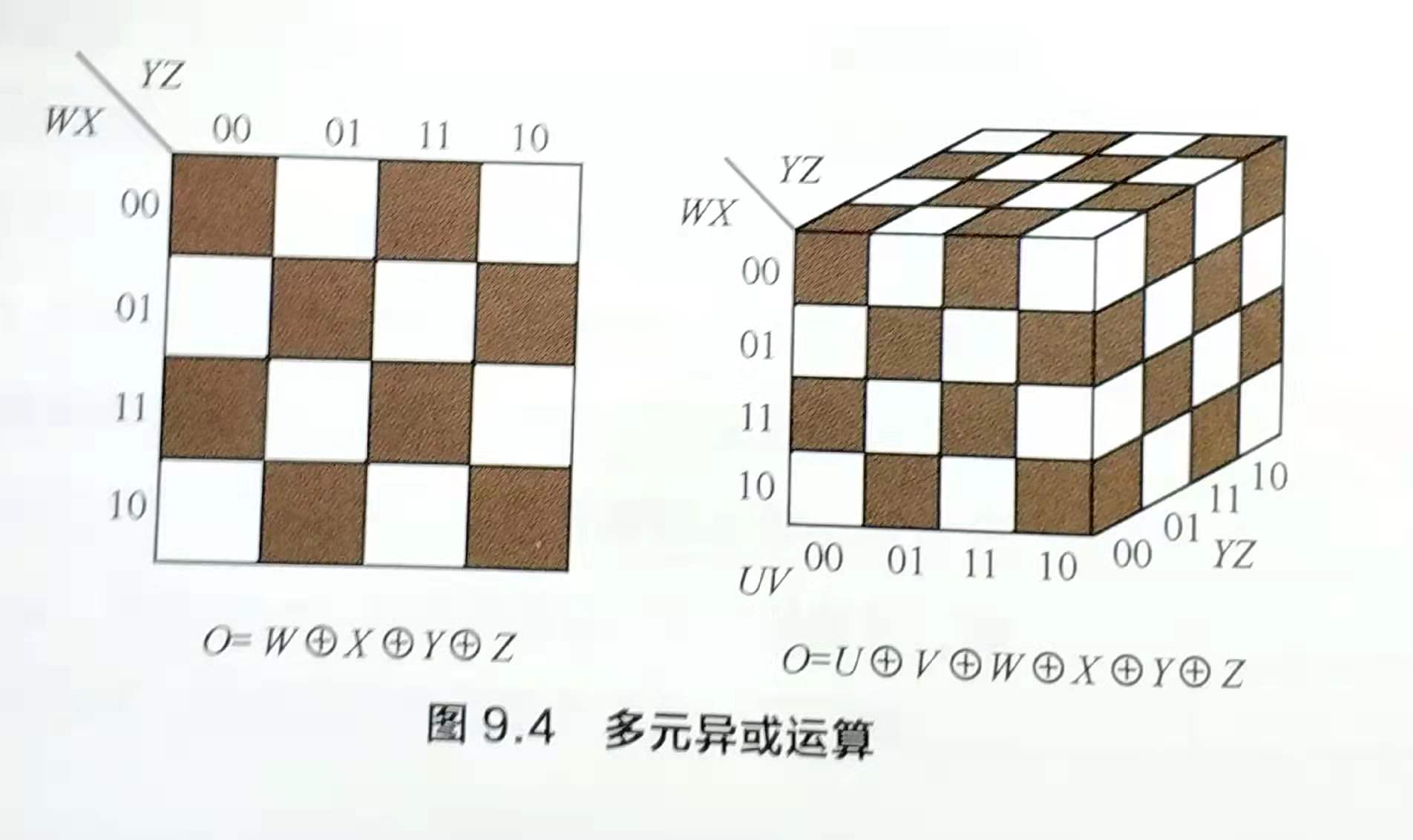
问题3
问:考虑多隐层的情况,实现包含n元输入的任意布尔函数最少需要多少个网络节点和网络层?
答:参考问题1的解答,考虑二元输入的情况,需要3个节点可以完成一次异或操作,其中隐藏层由两个节点构成,输出层需要一个结点,用来输出异或的结果并作为下一个结点的输入。对于四元输入,包含三次异或操作,需要3 * 3=9个节点即可完成。如下图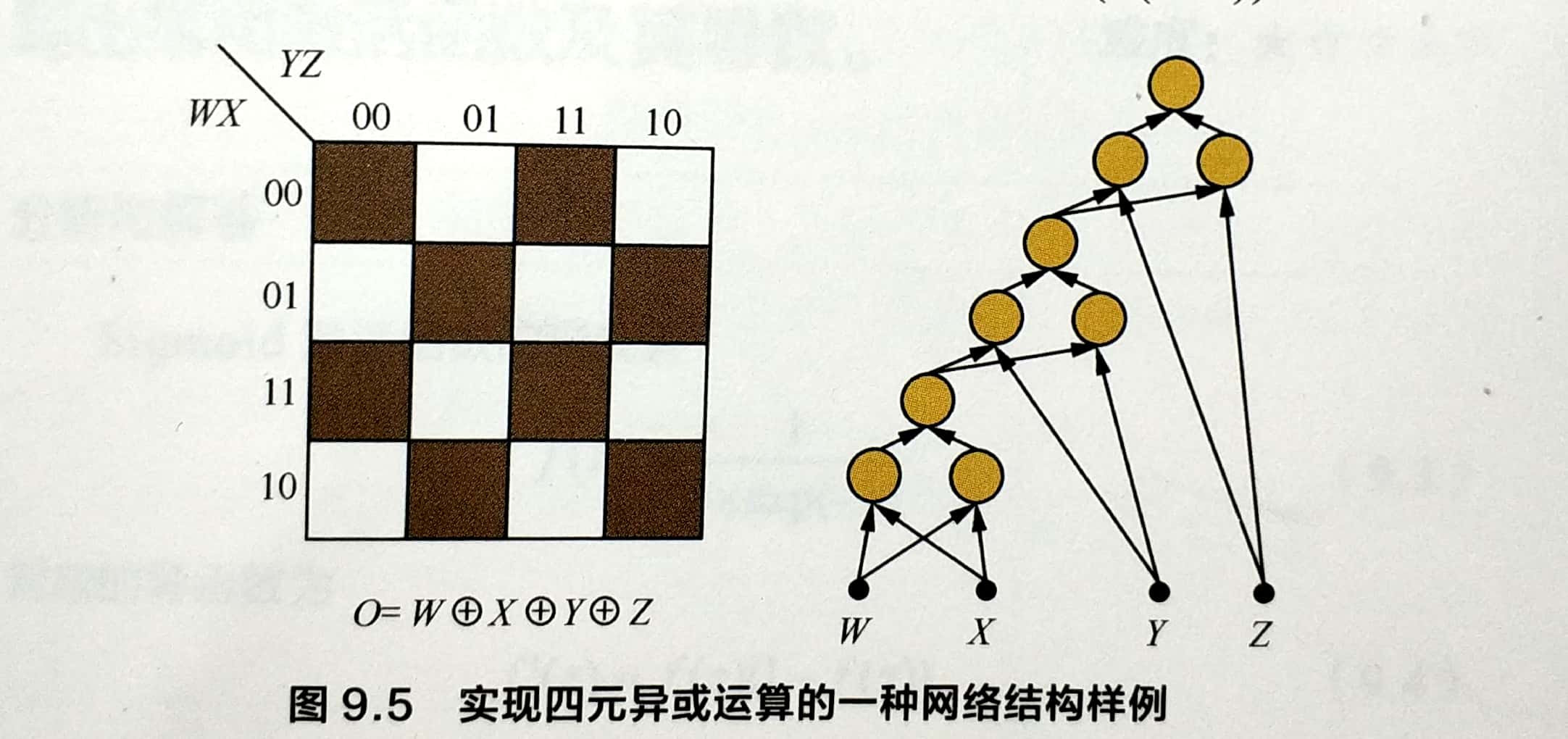
输入W,X,Y,Z四个布尔变量,首先用3个结点计算W异或X;然后再加入3个结点,将W,X的输出与Y进行异或,得到W异或X异或Y,最后与Z进行异或,整个网络总共需要9个结点。以此类推,n元异或函数需要包括3(n-1)个节点(包括最终输出节点)。多隐层结构可以将隐节点的数目从指数级O(2^(n-1))直接减少至线性级O(3(n-1))。
层数还可以进一步减小,如果在同一层中计算W异或X和Y异或Z,再将二者的输出进行异或就能将层数从6变成4,根据二分思想,每层节点两两分组进行异或运算,需要的最少网络层数为2log2N(向上取整)。
美团 深度学习技术发展历程
第一阶段 1943到1986年
1943年,人工神经元模型MCP(作者名字的缩写)的发明可以看做是人工神经网络的起点。MCP模型由多个输入加权求和,二值激活函数组成,通过网络来模拟神经元的过程。
1957年,感知机算法Perceptron的发明,使用MCP模型对多维输入做二分类,梯度下降法学习权重。感知机算法的思想很简单,即通过样本正确与否调整分类面,使得分类面对样本的分类误差最小。该算法是神经网络和支持向量机的基础,随后被证明能够收敛,其理论和实践效果引发了第一次神经网络浪潮。
1969年,美国数学家和人工智能先驱Minsky证明了感知机是一种线性模型,它只能处理线性分类问题,比如简单的异或问题(XOR)就解决不了。从而神经网络陷入了第一次近20年的停止期。
第二阶段 1986年到2006年
1986年,Hinton发明了优化多层感知机(MLP)的反向传播算法(BP)算法,从而解决了神经网络只能解决线性分类的问题,引发了第二轮研究热潮。三年后,就证明了MLP的万能逼近原理,也就是包含非线性隐层的MLP能逼近任意的联系函数,极大鼓舞了神经网络研究热情。
1990年,20世纪90年代,支持向量机如火如荼发展起来,理论上有很好的解释,且效果非常好。而神经网络开始走下坡路,一方面BP在深层网络中存在梯度消失和爆炸问题,另一方面其理论解释没那么完善,就这样神经网络一直低迷到2006年。
第三阶段 2006年至今
2006年。Hinton有了重大发明,提出的无监督分层初始化方法结合深度玻尔兹曼机解决了深层神经网络梯度消失等难题。这项发明发表在science期刊上,从而开启了深度学习第三次研究热潮。
2012年,ImageNet比赛夺冠AlexNet,引爆深度学习研究热潮。
2015年至今,各大公司纷纷开源其深度学习框架和模型,极大推进了各领域应用深度学习的进程。
统计学习方法 感知机
感知机(perceptron)是二类分类的线性分类模型,其输入为实例的特征向量, 输出为实例的类别,取+1和-1二值.感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面,属于判别模型.感知机学习旨在求出将训练数据进行线性划分的分离超平面,为此,导入基于误分类的损失函数,利用梯度下降法对损失函数进行极小化,求得感知机模型.感知机学习算法具有简单而易于实现的优点,分为原始形式和对偶形式.感知机预测是用学习得到的感知机模型对新的输入实例进行分类.感知机1957年由 Rosenblat提出,是神经网络与支持向量机的基础。
感知机模型

感知机是一种线性分类模型,属于判别模型。感知机模型的假设空间是定义在特征空间中的所有线性分类模型或线性分类器。
感知机的几何解释,线性方程wx+b=0,对于特征空间R中的一个超平面S,其中w是超平面的法向量,b是超平面的截距。这个超平面将特征空间划分为两个部分。位于两部分的点(特征向量)分别为正负两类,因此,超平面S被称为分离超平面。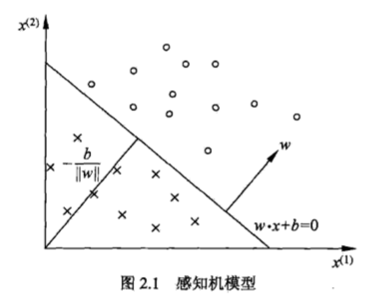
感知机学习的策略是极小化损失函数: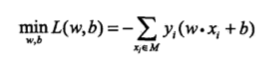
损失函数对应于误分类点到分离超平面的总距离。
感知机学习算法是基于随机梯度下降法的对损失函数的最优化算法,有原始形式和对偶形式.算法简单且易于实现.原始形式中,首先任意选取一个超平面,然后用梯度下降法不断极小化目标函数.在这个过程中一次随机选取一个误分类点使其梯度下降。