百面机器学习 逻辑回归
逻辑回归可以说是机器学习领域最基础也是最常用的模型,逻辑回归的原理推导以及扩展应用几乎是算法工程师的必备技能。
问题1
问:逻辑回归相比于线性回归,有何异同?
答:逻辑回归,乍一听名字和数学中的线性回归异派同源,但本质却是大相径庭。
首先,逻辑回归处理的是分类问题,线性回归处理的是回归问题,这是这两者最本质的区别。逻辑回归中,因变量取值是一个二元分布,模型学习得出的是E[y|x;θ],即给定自变量和超参数后,得到因变量的期望,并基于此期望来处理预测分类问题。
分类和回归是如今机器学习中两个不同的任务,而属于分类算法的逻辑回归,其命名有一定的历史原因。
将逻辑回归的公式进行整理,我们可以得到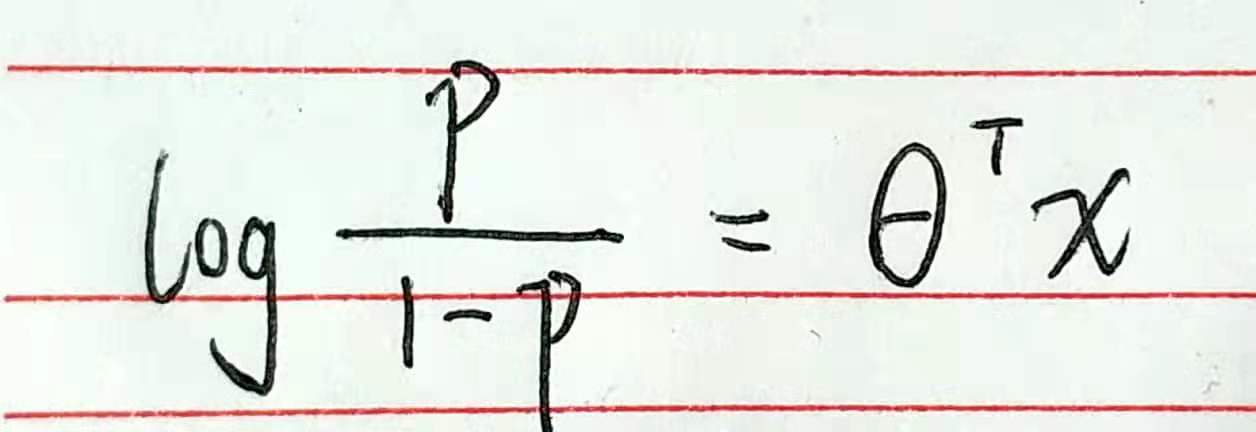
其中p=P(y=1|x),也就是将给定输入x预测为正样本的概率。如果把一个事件的几率定义为该事件发生的概率与该事件不发生的概率的比值 p / 1-p,那么逻辑回归可以看做是对于“y=1|x”这一事件的对数几率的线性回归,于是“逻辑回归”这一称谓也就延续下来了。
在关于逻辑回归的讨论中,我们均认为y是因变量,而非p / 1-p ,这便引出逻辑回归与线性回归最大的区别。即逻辑回归中的因变量为离散的,而线性回归中的因变量是连续的。并且在自变量x与超参数θ确定的情况下,逻辑回归可以看作广义线性模型在因变量y服从二元分布时的一个特殊情况;而使用最小二乘法求解线性回归时,我们认为因变量y服从正态分布。
相同之处:首先二者都使用了极大似然估计来对训练样本进行建模。线性回归使用最小二乘法,实际上就是在自变量x与超参数θ确定,因变量y服从正态分布的假设下,使用极大似然估计的一个化简;而逻辑回归中通过对似然函数的学习,得到最佳参数θ。另外,二者在求解超参数过程中,都可以使用梯度下降的方法,这也是监督学习中一个常见的相似之处。
问题2
问:当使用逻辑回归处理多标签的分类问题时,有哪些常见做法,分别应用于哪些场景,它们之间又有着怎样的关系?
答:使用哪一种方法来处理多分类的问题取决于具体问题的定义。首先,如果一个样本只对应于一个标签,我们可以假设每个样本属于不同标签的概率服从于几何分布,使用多项逻辑回归(Softmax Regression)来进行分类。多项逻辑回归实际上是二分类逻辑回归在多标签分类下的一种扩展。
当存在样本可能属于多个标签的情况时,我们可以训练k个二分类的逻辑回归分类器。第i个分类器用以区分每个样本是否可以归为第i类,训练该分类器时,需要把标签重新整理为“第i类标签”与“非第i类标签”两类。通过这样的办法,我们就解决了每个样本可能拥有多个标签的情况。
美团机器学习实践
逻辑回归是一种广义线性模型,它与线性回归模型包含的线性函数十分相似。但逻辑回归通过对数概率函数将线性函数的结果进行映射,目标函数的取值空间从(-∞,+∞)映射到(0,1)。从而可以处理分类问题。逻辑回归虽然有“回归”二字,却是统计学习中经典分类方法。
逻辑回归原理
将线性回归与逻辑回归进行对比,可以发现线性回归模型在训练时在整个实数域上对异常点的敏感性是一致的,因而在处理分类问题时线性回归模型效果较差,线性回归模型不适合处理分类问题。对于二分类任务,逻辑回归输出标记y∈{0,1},而线性回归模型产生的预测值是实数,所以需要一个映射函数将实值转换为0 / 1值。
最理想的映射函数是单位阶跃函数,即预测值大于零就判为正例,预测值小于零则判为负例,预测值为临界值则可任意判别。虽然单位阶跃函数看似完美解决了这个问题,但是单位阶跃函数不连续并且不充分光滑,因而无法进行求解。
所以我们希望找到一个近似函数来替代单位阶跃函数,并希望它单调可微。对数概率函数正是这样一个替代的函数,对数概率函数将θ^Tx(θTx是多项式)的值转化为接近0或1的值,并且其输出=0处变化很陡,将对数概率函数代入,就能得到逻辑回归的表达式。
在进行分类的过程实际上是使用多项式来进行“围数据”,逻辑回归相对于在多项式上加了一层函数,输出0,1。
为了提高算法收敛速度和节省内存,实际应用在迭代求解时往往会使用高效的优化算法,如LBFGS,信赖域算法,但这些求解方法是基于批量处理的,批处理算法无法高效处理超大规模的数据集,也无法对线上模型进行快速实时更新。
随机梯度下降是相对于批处理的另外一种优化方式,它每次只用一个样本来更新模型的权重,这样就可以更快地进行模型迭代。对于广告和新闻推荐这种数据和样本更新比较频繁场景,快速的模型更新能够更早捕捉到新数据的规律进而提升业务指标。谷歌FTRL就是基于随机梯度下降的一种逻辑回归优化算法。是一种在线学习算法。
逻辑回归应用
逻辑回归常用于疾病自动诊断,经济预测,点击率预测等领域。由于其处理速度快且容易并行,逻辑回归适合用来学习需要大规模训练的样本和特征,对于广告十亿量级的特征和亿量级的特征来说,逻辑回归有着天然的优势,因而逻辑回归在工业界获得了广泛的应用。而逻辑回归的缺点是需要大量的特征组合和离散工作来增加特征的表达性,模型表达能力弱,比较容易欠拟合。
业界对逻辑回归的研究热点主要集中在稀疏性,准确性和大规模计算上。实际应用逻辑回归前,经常会对特征进行独热(One Hot)编码,比如广告点击率应用中的用户ID,广告ID。为了实现计算效率和性能优化,逻辑回归求解有很多种优化方法,比如BFGS,LBFGS,共轭梯度法,信赖域法,其中前两个是牛顿法的变种,LBFGS算法是BFGS算法在受限内存下的近似优化。针对逻辑回归在线学习中遇到的稀疏性和准确性问题,谷歌和伯克利分校提出来稀疏性比较好的FOBOS算法,微软提出了RDA算法。谷歌综合了精度比较好的RDA和稀疏性比较好的FTRL,但在L1范数或者非光滑的正则项下,FTRL的效果会更好。
在实际应用中,逻辑回归也需要注意正则化的问题。L1正则(也称LASSO)假设模型参数取值满足拉普拉斯分布,L2正则(也称RIDGE)假设模型参数取值满足高斯分布。