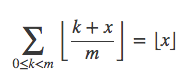取整基础
符号定义
向下取整函数⌊x⌋定义为小于等于x的最大整数。
向上取整函数⌈x⌉定义为大于等于x的最小整数。
{x}定义为实数x的小数部分,即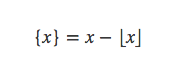
性质
性质1
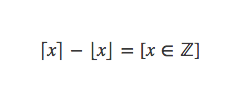
表示x是整数则取0,x不是整数则取1。
性质2
取整函数范围: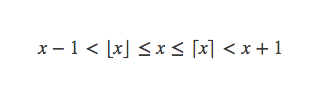
性质3
负数的取整: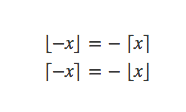
性质4
取整函数中的整数可以提取出来:
应用
应用1
证明: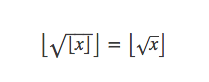
更一般的,我们还可以证明,对于任意连续、递增的函数f(x),如果它满足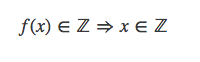
那么有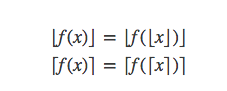
我们证明第2个式子,第1个同理可证。
如果x=⌈x⌉,显然成立。
否则x<⌈x⌉,因为f(x)递增,所以有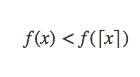
两边同时取整,有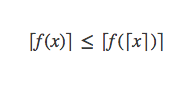
若是想要证左右两边相等,只需要证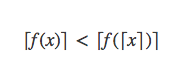
不成立即可。
假设上式成立,那么由中间值定理,一定存在x≤y<⌈x⌉,使得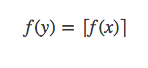
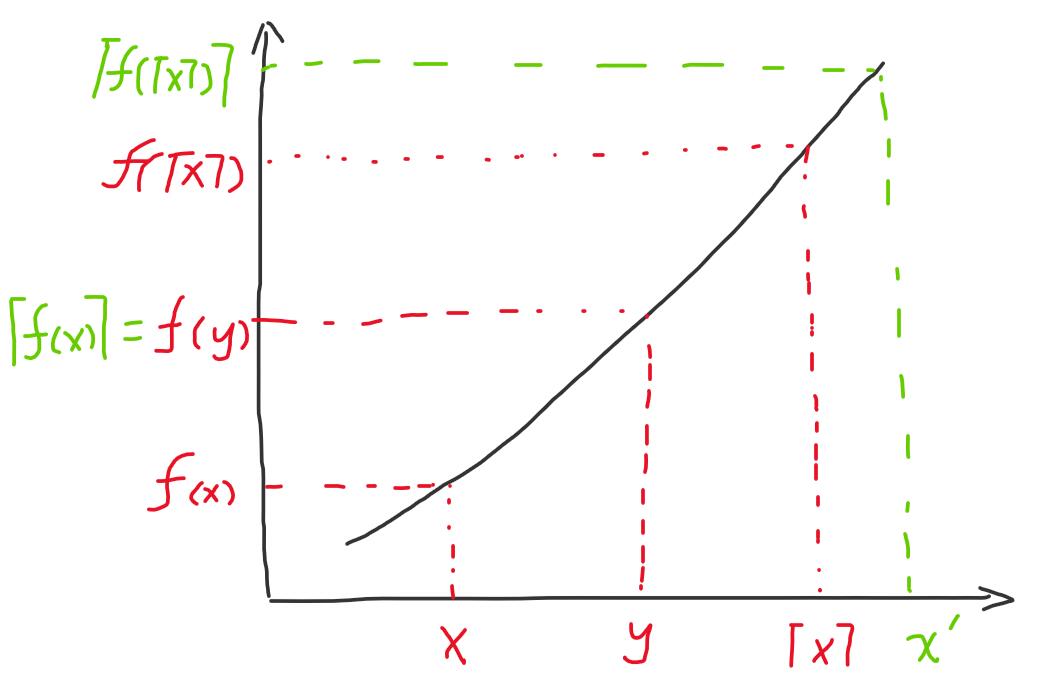
由上图可以看出,当下面式子成立时,满足中间值定理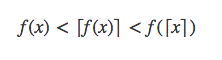
但是,我们假设是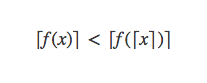
那么由⌈f(x)⌉<⌈f(⌈x⌉)⌉能否推出⌈f(x)⌉<f(⌈x⌉)呢?当然是可以的。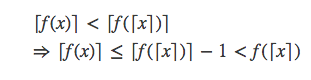
所以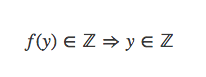
(怎么得到的。。)
又因为x≤y<⌈x⌉,所以不存在整数y,矛盾!
所以证得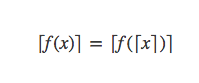
另一个特殊的例子是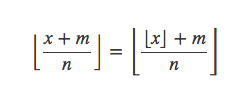
其中m和n都是整数,并且n是正整数。
应用2
求1到1000中使得下列式子成立的n一共有多少个?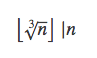
求解方法如下: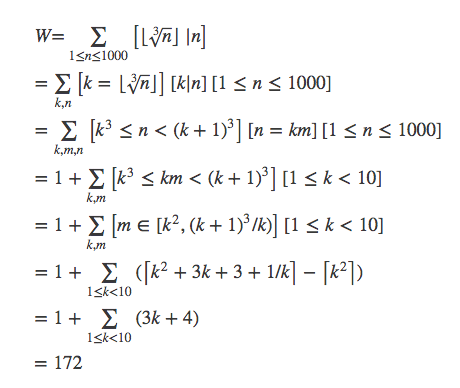
继续推广,求1到N中使得上面式子成立的n有多少个,令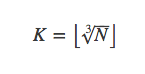
也就是小于等于的最大整数。所以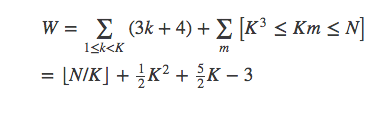
渐进地等于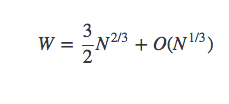
应用3
定义一个实数的谱为: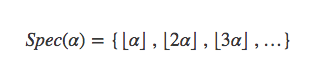
很容易证明如果两个实数α≠β,那么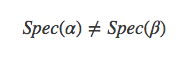
假设α<β,那么令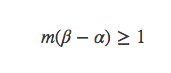
所以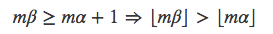
所以集合Spec(β)中小于⌊mα⌋的元素个数小于m。而集合Spec(α)中小于⌊mα⌋的元素个数大于等于m。所以两个集合不相等。
谱有很多奇妙的性质,例如下面两个谱: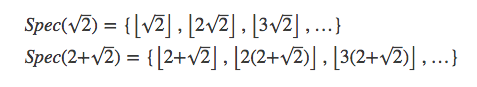
可以发现,这两个谱正好划分了正整数集。
证明方法也很简单,只要证明对任意正整数n,两个集合中小于n的元素个数之和为n,过程如下: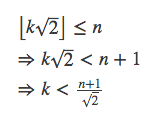
所以第一个集合中小于n的元素个数为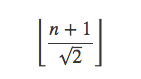
同理第二个集合中小于n的元素个数为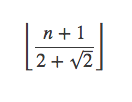
所以总个数为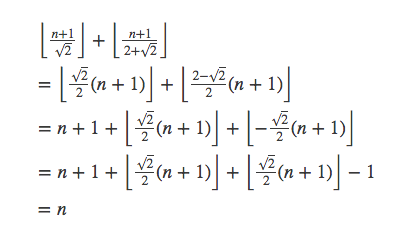
得证。
取整进阶
约瑟夫环新解
这里我们继续推广到一般情况,如果有n个人,每隔q个人踢掉一个人,最后剩下的是几号?初始编号为1…n,现在考虑一种新的编号方式。第一个人不会被踢掉,编号加1,变成n+1,然后第二个人编号变为n+2,直到第q个人,他被踢掉了。然后第q+1个人编号继续加1,变成了n+q,依次下去。考虑当前踢到的人编号为kq,那么此时已经踢掉了k个人,所以接下去的人新的编号为n+k(q−1)+1…。所以编号为kq+d的人编号变成了n+k(q−1)+d,其中1≤d<q。直到最后,可以发现活下来的人编号为qn,问题是怎么根据这个编号推出他原来的编号?以n=10,q=3为例,下图就是每个人新的编号:
令
N=n+k(q−1)+d
所以他上一次的编号是
kq+d=kq+N−n−k(q−1)=k+N−n
因为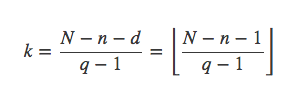
所以上一次编号可以写为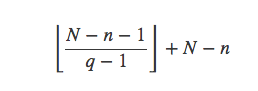
如果我们用D=qn+1−N替代N,将会进一步简化算法: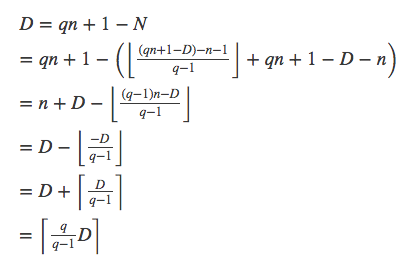
模的性质
定义与性质
模定义如下: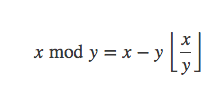
特别的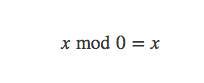
与此类似,定义一个与模类似的运算: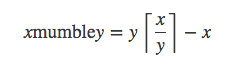
模有一些性质: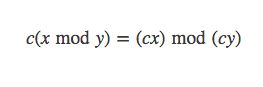
应用
考虑如下问题,怎么平均分配n个东西给m个人?很容易想到,首先分给每个人⌊n/m⌋个东西,剩下n mod m件东西分给前n mod m个人,一人多一件就行。概括起来就是,前n mod m个人,每人⌈ n / m⌉件,剩下的人,每人⌊n / m⌋件。统一表示呢?有的,每个人分到的件数为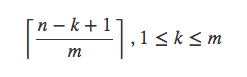
为什么呢?假设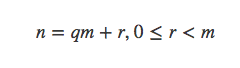
那么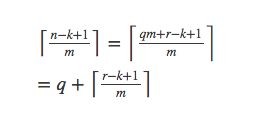
当1≤k≤r时,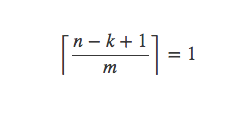
当r<k≤m时,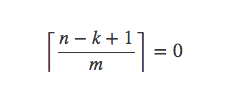
得证,因此可以得到如下等式: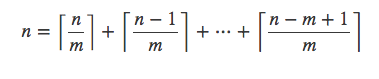
由n=⌊n / 2⌋+⌈n / 2⌉
可以进一步将其转换为下取整形式: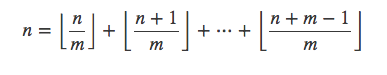
令n=⌊mx⌋
我们得到了一个令人惊奇的等式: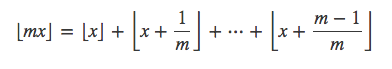
习题
题3
题目:求⌊nx⌋=n⌊x⌋的充要条件。
解答:
因为x=⌊x⌋+{x},所以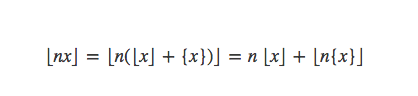
要使得⌊nx⌋=n⌊x⌋,就必须有⌊n{x}⌋=0,所以n{x}<1即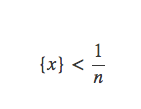
题7
题目:求下列递推式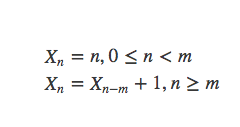
解答:
因为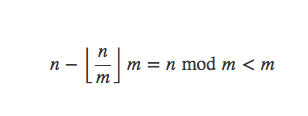
所以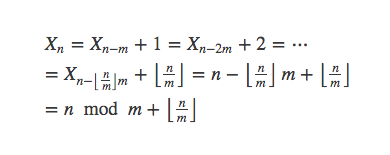
题8
题目:n个物品放到m个盒子中,求证至少有一个盒子物品数大于等于⌈n / m⌉,至少有一个盒子物品数小于等于⌊n / m⌋。
解答:假设所有的盒子物品数都小于⌈n / m⌉,那么总物品数S满足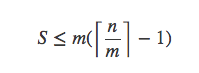
令n=qm+r,0≤r<m,那么有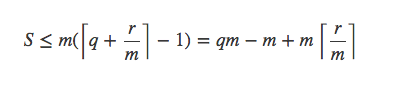
如果r=0,那么有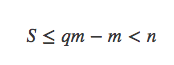
如果r>0,那么有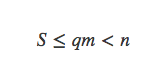
这与S=n矛盾!所以至少有一个盒子物品数大于等于⌈n / m⌉。
假设所有的盒子物品数都大于⌊n / m⌋,那么总物品数S满足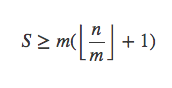
令n=qm+r,0≤r<m,那么有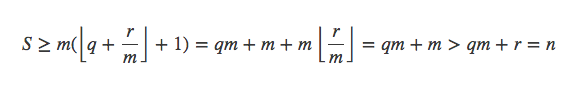
这与S=n矛盾!所以至少有一个盒子物品数小于等于⌊n / m⌋。
取整进阶
例题1
求和: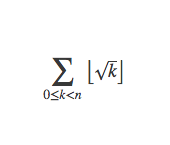
方法一
首先令m=⌊√k⌋
那么有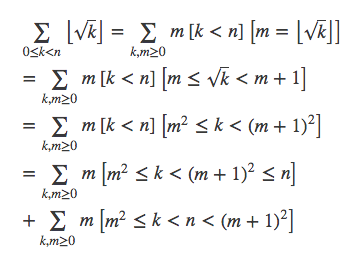
我们先算左半部分,先假设n=a的2次方,那么有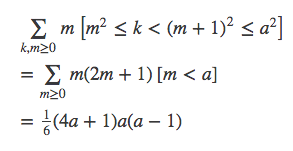
而对于一般的n,令a=⌊√n⌋,我们只需要计算a的2次方≤k<n的部分,而这部分√k=a,所以结果为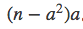
所以总的结果为: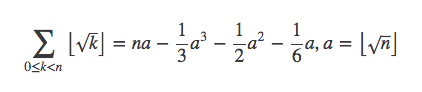
为什么没有算右半部分?因为右半部分就是a2≤k<n的这部分,已经计算过了。
方法2

定理1
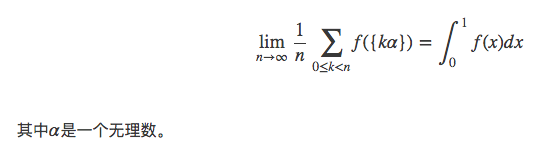
这个公式说明了,无理数α的整数倍的小数部分均匀分布在(0,1)之间。这就给了我们一个启示,我们可以用它来生成随机数啊!其他用处还有很多。
例题2
求如下和式: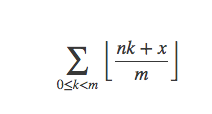
其中整数m>0,n也是整数。
通过枚举m=1,2,3,…,可以发现和式满足如下形式: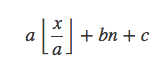
如何进行计算:
首先做一个变形: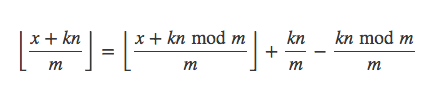
这就将原来的和式分为了三个部分求和。
第一个部分为: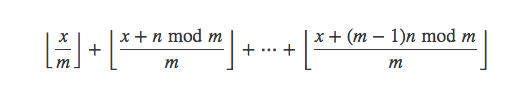
这里通过枚举可以发现它的值是有周期的,周期重复次数是d=gcd(m,n)。所以算出来结果为: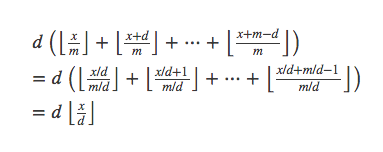
第二个部分为: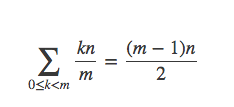
第三个部分为: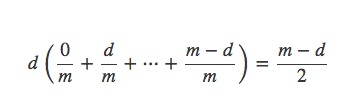
所以总的结果为: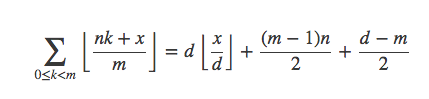
对结果稍稍变形,可以得到另一个结果: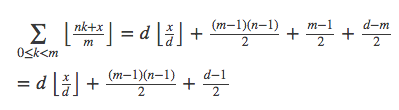
可以发现,m和n是对称的!所以可以得到如下结论: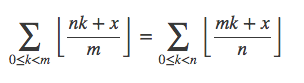
这有什么用呢?当m特别大、n很小的时候可以大大减少项的个数!
如果我们令n=1,就会发现,得到的式子和之前证过的一个式子一模一样!