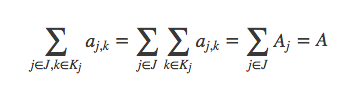求递推式本身的表达式
将递归式转化为求和再求出递推式本身的表达式。
考虑如下递归式: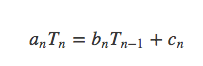
两边同时乘以sn得到: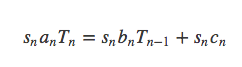
观察Tn项和Tn-1项之前的系数,要想转化为可以求和的递归式,必须有: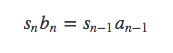
即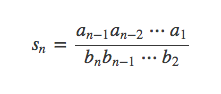
此时令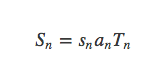
得到: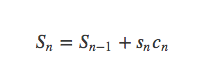
此时再求和可得: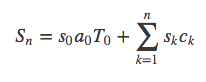
所以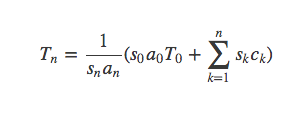
例题1
设n个数快速排序的操作次数为Cn,那么有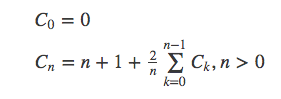
用n-1取代n可以得到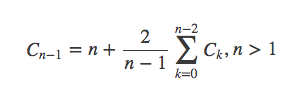
两式相减可以得到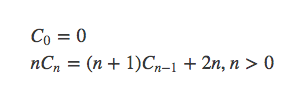
观察形式,由上面方法可以得到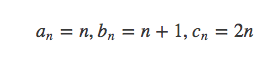
所以得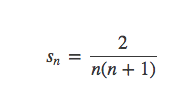
进而带入公式。可以求得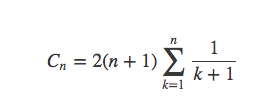
其中调和级数为: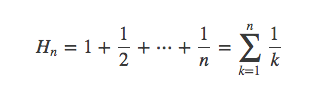
所以最后结果为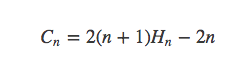
求和三大定律
结合律、分配率、交换律。
例题2
求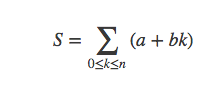
这里使用求和定律来做
用n-k取代k,得到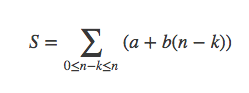
即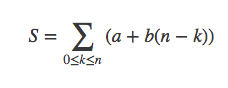
两式相加得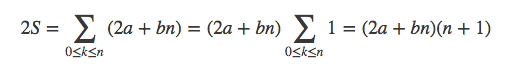
所以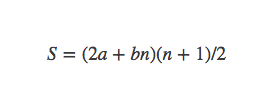
例题3
求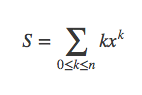
这里用到另一种求和的方法。
两边同时加上第n+1项,得到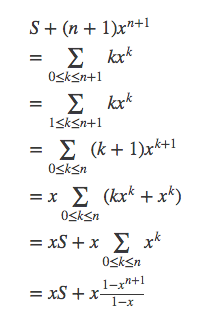
所以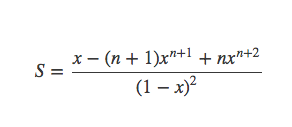
还可以这样求解: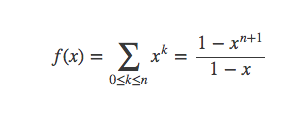
求导得到: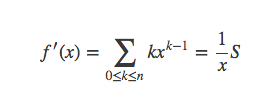
所以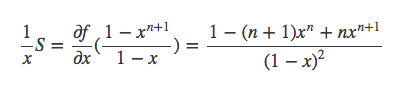
同样可以得到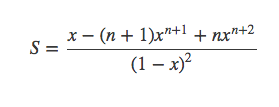
多重求和
多重求和,也就是一个和式由多个下标来指定。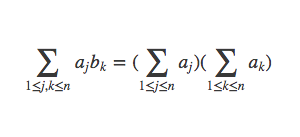
例题1
一个对称矩阵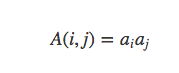
求: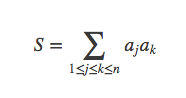
这是这个矩阵的上三角加对角线求和,因为是对称的嘛,可以补全下三角,加上对角线就行了。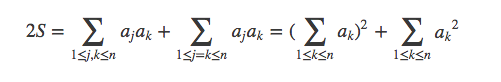
所以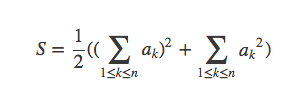
例题2
有如下式子,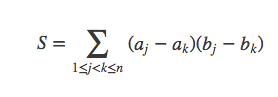
调换j,k位置,得到: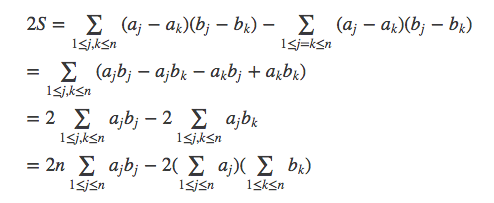
所以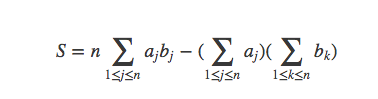
至此解完,可以推出一个著名不等式—-切比雪夫不等式: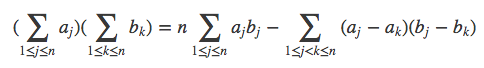
例题3
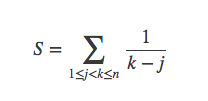
使用三种方法解这个式子:
调和级数
调和级数: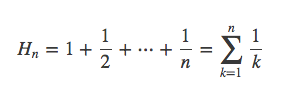
方法一
首先将j和k分开,首先计算对j求和: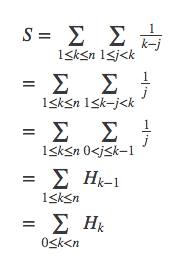
方法二
先计算对k求和: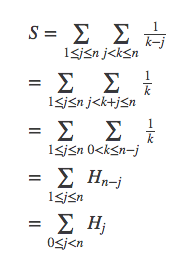
方法三
按对角线求和: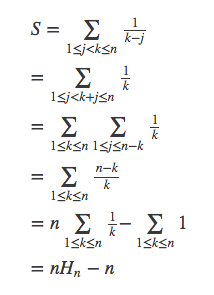
由此得到了一个完全不同的表示形式,所以得到了: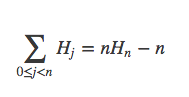
几种求和方法
针对以下求和式,使用八种方法来求解: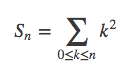
它的答案为: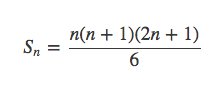
扰动法
令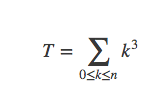
所以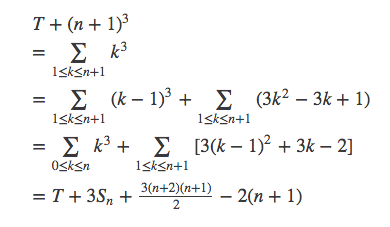
解出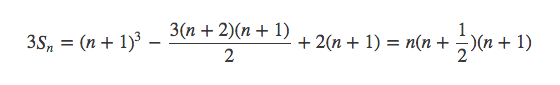
最终得到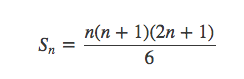
可以看出,我们本来是要对k的二次方求和的,但是只要对k的三次方用扰动法求和即可,因为求和过程中k的三次方项会被抵消掉。
扩展成二重指标求和
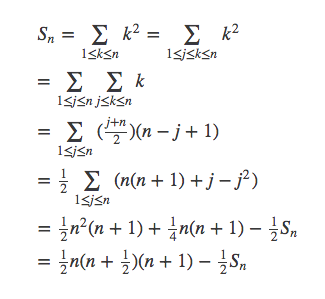
用有限微分求和
微分的形式为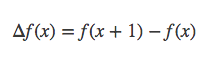
如果定义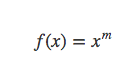
则有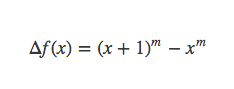
似乎不能和导数形式统一起来,用起来也不方便,定义一个新的函数,叫下降阶乘幂: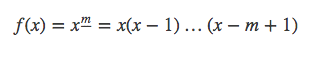
这个函数有一个很好的性质,那就是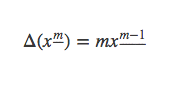
令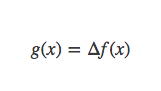
和积分类似,有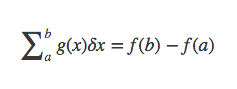
所以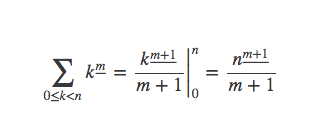
因为有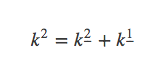
所以有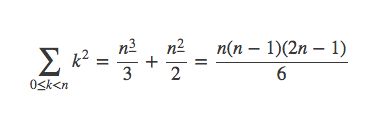
同样可以得到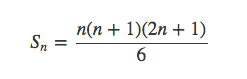
下降阶乘幂
性质一

性质二
给出下降阶乘幂为负数的定义: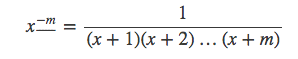
性质三

性质四
定义下降阶乘幂的好处就是为了求差分方便,下降阶乘幂的差分为: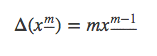
类比不定积分,不定和为: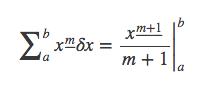
但是这里m≠−1,若是m=−1,直接运用差分定义可以求出: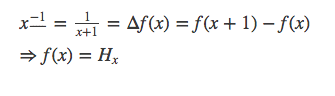
所以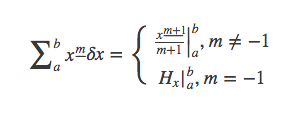
性质五
什么函数的差分是自身。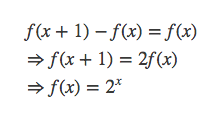
进一步推广可得: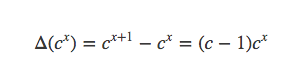
所以得到一种新的等比数列计算方法: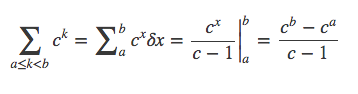
性质六
结合律和分配率在差分运算中也适用。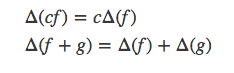
性质七
类似分部积分,这里也可以分部来求差分。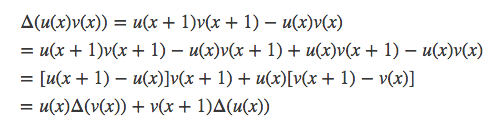
给出一个新的记号移位运算: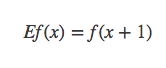
所以得到了差分的分部运算法则: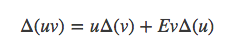
对两边求和,又可以得到不定求和的分布运算法则: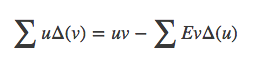
例一
计算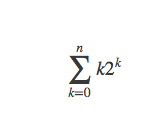
首先计算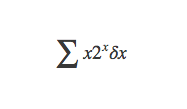
这里可以令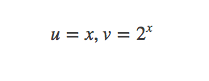
所以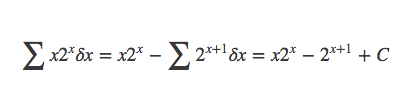
求和式就可以转化为不定求和来算了: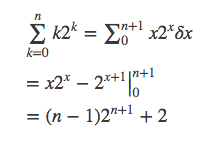
例二
计算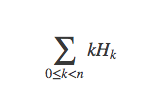
首先计算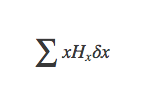
这里注意要令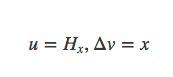
不能倒过来,因为Hx的不定和很难求出来。所以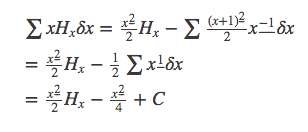
所以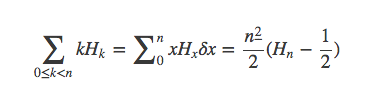
无限求和
之前求和式。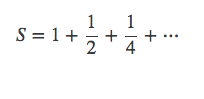
两边同时乘2,得: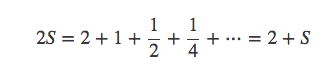
解得: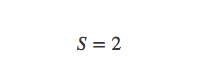
但是同样的方式计算式子: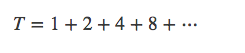
两边同时乘2,得: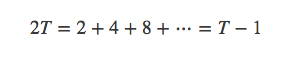
解出: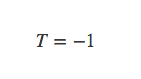
显然是不可能的,因为这里T是发散的,所以不能这么求。

比如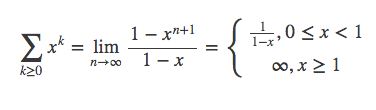
再如: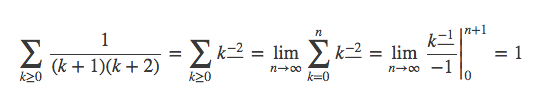
求有正有负的和式。
可以考虑用不同的配对,将正负组合在一起,从而相消求和。
我们可以将正数和负数分开求和,因为正数求和已经解决了。定义: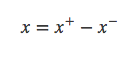
其中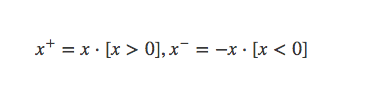
求和式对两部分分别求和: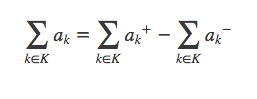
最后可以推广到二重求和。