已修改
人工智能课上内容
贝叶斯概率vs经典概率
关于统计推断的主张和想法,大体可以纳入到两个体系之内,其一叫频率学派,其特征是把需要推断的参数θ视作固定且未知的常数,而样本X是随机的,其着眼点在样本空间,有关的概率计算都是针对X的分布。另一派叫做贝叶斯学派,他们把参数θ视作随机变量,而样本X是固定的,其着眼点在参数空间,重视参数θ的分布,固定的操作模式是通过参数的先验分布结合样本信息得到参数的后验分布。
经典概率
即我们学习的概率论呀。
方法:MLE(极大似然估计)
认为世界是确定的。θ是唯一的。
贝叶斯概率
方法:MAP(最大后验估计)
频率派认为估计对象(参数)是一个未知的固定值。而贝叶斯却认为未知的参数都是随机变量。
我们要通过一些事实估计“爱因斯坦在1905年12月25日晚上八点吸烟”的真假。定义参数:,吸烟;,没吸烟。那么频率派认为,爱因斯坦有没有曾经在这时刻吸烟是事实,是取值0或者1的固定数,不能说”=1的概率是xxx”;然而贝叶斯派认为可以说“=1概率是30%”。而且随着所得资料(样本x)的增多,我们可以把这个概率加以变化,记得到的分布。这个概率其实是“信心”的含义。
后验(输出)=先验(输入)*似然(输入)
贝叶斯思想的优势
1、 对于某一种独立重复随机事件,如果采用最大似然法计算出两个极值点,例如99、100,此时最大似然法只会取最大值点100的概率值。但是使用贝叶斯思想,我们就可以同时考虑极值点99、100的概率。
在实际应用中,事件A的概率可能不是一成不变的(实验难以重复独立,或者事件A的概率就是随机的)。比如考虑一个人生病的概率,幼年时生病概率高,中年时生病概率低,老年时生病概率高,或者冬天生病概率高,夏天生病概率低。频率派思想认为的概率是事件A的固定属性在这些状况下就不适用。严格的来说,任何场景下你都无法保证事件A概率是固定的。
2、 频率派使用的最大似然法,只能得到概率的最大似然估计。但是通过贝叶斯公式得到概率后验分布函数后,我们可以进行各种处理,比如取概率期望,概率中位数,概率极大值等等。
后验分布
以前我们想知道一个参数,要通过大量的观测值才能得出,而且是只能得出一个参数值。而现在运用了贝叶斯统计思想,这个后验概率分布其实是一系列参数值的概率分布,再说简单点就是我们得到了许多个参数及其对应的可能性,我们只需要从中选取我们想要的值就可以了:有时我们想要概率最大的那个参数,那这就是 后验众数估计(posterior mode estimator);有时我们想知道参数分布的中位数,那这就是 后验中位数估计(posterior median estimator);有时我们想知道的是这个参数分布的均值,那就是 后验期望估计。这三种估计没有谁好谁坏,只是提供了三种方法得出参数,看需要来选择。现在这样看来得到的参数是不是更具有说服力?
先验分布
说完了后验分布,现在就来说说先验分布。先验分布就是你在取得实验观测值以前对一个参数概率分布的 主观判断,这也就是为什么贝叶斯统计学一直不被认可的原因,统计学或者数学都是客观的,怎么能加入主观因素呢?但事实证明这样的效果会非常好!再拿掷硬币的例子来看(怎么老是拿这个举例,是有多爱钱。。。),在扔之前你会有判断正面的概率是50%,这就是所谓的先验概率,但如果是在打赌,为了让自己的描述准确点,我们可能会说正面的概率为0.5的可能性最大,0.45的几率小点,0.4的几率再小点,0.1的几率几乎没有等等,这就形成了一个先验概率分布。
你这个硬币的材质是不均匀的,那正面的可能性是多少呢?这就让人犯糊涂了,我们想有主观判断也无从下手,于是我们就想说那就先认为0~1之间每一种的可能性都是相同的吧,也就是设置成0~1之间的均匀分布 作为先验分布吧,这就是贝叶斯统计学当中的 无信息先验(noninformative prior)!那么下面我们就通过不断掷硬币来看看,这个概率到是多少,贝叶斯过程如下: (图来自[3])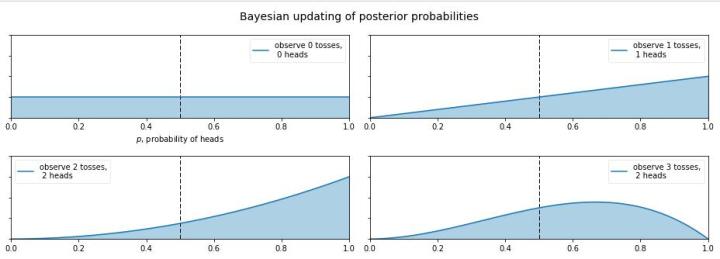
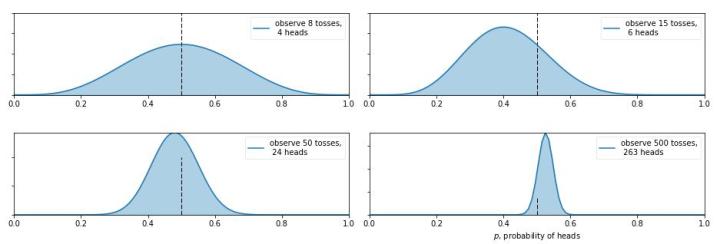
从图中我们可以看出,0次试验的时候就是我们的先验假设——均匀分布,然后掷了第一次是正面,于是概率分布倾向于1,第二次又是正,概率是1的可能性更大了,但 注意:这时候在0.5的概率还是有的,只不过概率很小,在0.2的概率变得更小。第三次是反面,于是概率分布被修正了一下,从为1的概率最大变成了2/3左右最大(3次试验,2次正1次反当然概率是2/3的概率最大)。再下面就是进行更多次的试验,后验概率不断根据观测值在改变,当次数很大的时候,结果趋向于0.5(哈哈,结果这还是一枚普通的硬币,不过这个事件告诉我们,直觉是不可靠的,一定亲自实验才行~)。有的人会说,这还不是在大量数据下得到了正面概率为0.5嘛,有什么好稀奇的? 注意了!画重点了!(敲黑板) 记住,不要和一个统计学家或者数学家打赌!跑题了,跑题了。。。说回来,我们上面就说到了古典概率学的弊端就是如果掷了2次都是正面,那我们就会认为正面的概率是1,而在贝叶斯统计学中,如果我们掷了2次都是正面,只能说明正面是1的可能性最大,但还是有可能为0.5, 0.6, 0.7等等的,这就是对古典统计学的一种完善和补充,于是我们也就是解释了,我们所谓的 地震的概率为5%;生病的概率为10%等等这些概率的意义了,这就是贝叶斯统计学的哲学思想。
所以贝叶斯得到的是θ的分布。
贝叶斯分析
贝叶斯分析的思路对于由证据的积累来推测一个事物发生的概率具有重大作用, 它告诉我们当我们要预测一个事物, 我们需要的是首先根据已有的经验和知识推断一个先验概率, 然后在新证据不断积累的情况下调整这个概率,整个通过积累证据来得到一个事件发生概率的过程我们称为贝叶斯分析。
贝叶斯决策如果一旦变成自动化的计算机算法, 它就是机器学习。
统计学习方法 朴素贝叶斯法
朴素贝叶斯法的学习与分类
基本方法
注意:朴素贝叶斯法与贝叶斯估计是不同的概念。
朴素贝叶斯法对条件概率分布作了条件独立性的假设.由于这是一个较强的
假设, 朴素贝叶斯法也由此得名.具体地,条件独立性假设是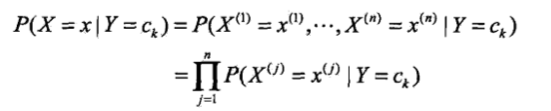
朴素贝叶斯法实际上学习到生成数据的机制,所以属于生成模型.条件独立假设等于是说用于分类的特征在类确定的条件下都是条件独立的.这一假设使朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
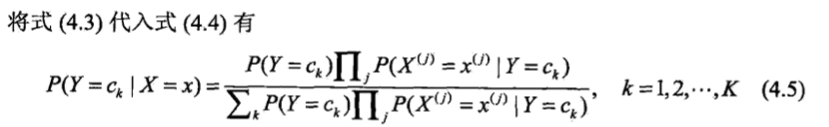
这是朴素贝叶斯法分类的基本公式,于是,朴素贝叶斯分类器可表示为: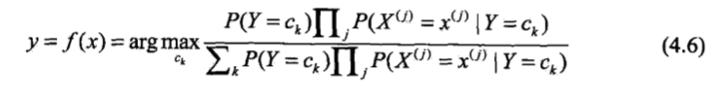

后验概率最大化的含义
朴素贝叶斯法将实例分到后验概率最大的类中.这等价于期望风险最小化.假设选择0-1损失函数: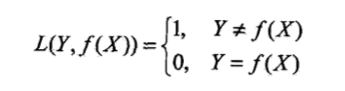


朴素贝叶斯的参数估计
极大似然估计

学习与分类算法
朴素贝叶斯算法(naive Bayes algorithm)

例

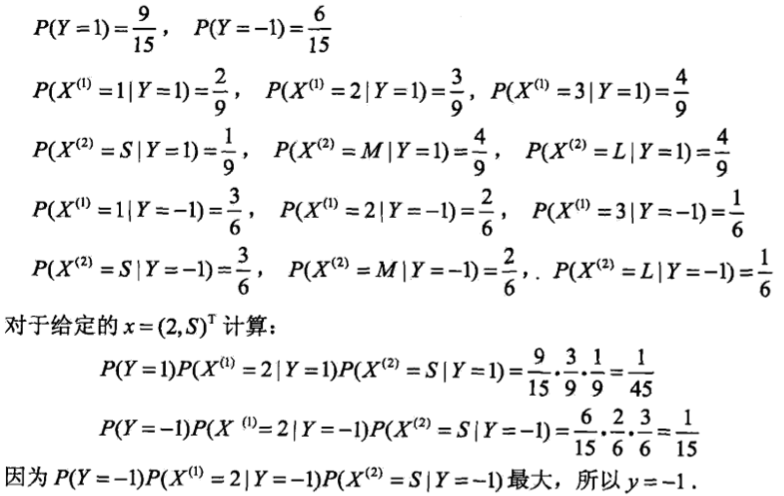
贝叶斯估计

例

西瓜书 关于朴素贝叶斯分类器的补充
在现实任务中朴素贝叶斯分类器有多种使用方式.例如,若任务对预测速度要求较高,则对给定训练集,可将朴素贝叶斯分类器涉及的所有概率估值事先计算好存储起来,这样在进行预测时只需“查表”即可进行判别;若任务数据更替频繁,则可采用“懒惰学习”(lazy learning) 方式,先不进行任何训练,待收到预测请求时再根据当前数据集进行概率估值;若数据不断增加,则可在现有估值基础_上,仅对新增样本的属性值所涉及的概率估值进行计数修正即可实现增量学习。
西瓜书 半朴素贝叶斯分类器
为了降低贝叶斯公式中估计后验概率P(c|x)的困难,朴素贝叶斯分类器采用了属性条件独立性假设,但在现实任务中这个假设往往很难成立.于是,人们尝试对属性条件独立性假设进行一定程度的放松,由此产生了一类称为“半朴素贝叶斯分类器”(semi-naive Bayes clasifers)的学习方法。
半朴素贝叶斯分类器的基本思想是适当考虑一部分属性间的互相依赖信息,从而既不需要进行完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系。“独依赖估计”(One-Dependent Estimator,简称ODE)是半朴素贝叶斯分类器最常用的一种策略。顾名思义,所谓“独依赖”就是假设每个属性在类别之外最多仅依赖一个其他属性,即:
于是,问题的关键就转化为如何确定每个属性的父属性,不同的做法产生不同的独依赖分类器
最直接的做法是假设所有属性都依赖同一个属性,称为“超父”(super-parent),然后通过交叉验证等模型选择方法来确定超父属性,由此形成了SPODE方法。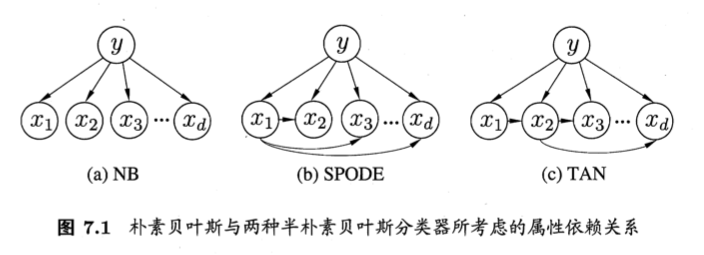
按下不表
西瓜书 贝叶斯网
贝叶斯网亦称“信念网”,它借助有向无环图(Directed Acyclic Graph,简称DAG)来刻画属性间的依赖关系,并使用条件概率表(Conditional Probability Table,简称CPT)来描述属性的联合概率分布。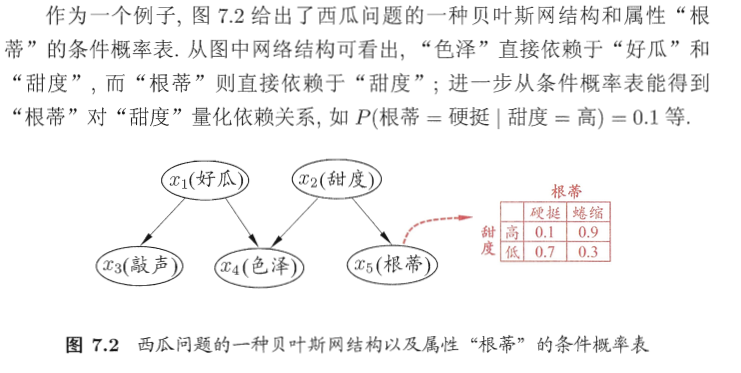
按下不表。
博客
贝叶斯推断
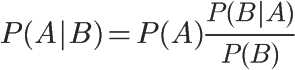
P(A)称为”先验概率”(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为”后验概率”(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为”可能性函数”(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
这就是贝叶斯推断的含义。我们先预估一个”先验概率”,然后加入实验结果,看这个实验到底是增强还是削弱了”先验概率”,由此得到更接近事实的”后验概率”。
在这里,如果”可能性函数”P(B|A)/P(B)>1,意味着”先验概率”被增强,事件A的发生的可能性变大;如果”可能性函数”=1,意味着B事件无助于判断事件A的可能性;如果”可能性函数”<1,意味着”先验概率”被削弱,事件A的可能性变小。
要知道我们只需要比较 P(H1|E)和P(H2|E)的大小,找到那个最大的概率就可以。既然如此,两者的分母都是相同的,那我们只需要比较分子即可。即比较P(E|H1)P(H1)和P(E|H2)P(H2)的大小,所以为了减少计算量,全概率公式在实际编程中可以不使用。
其中P(B):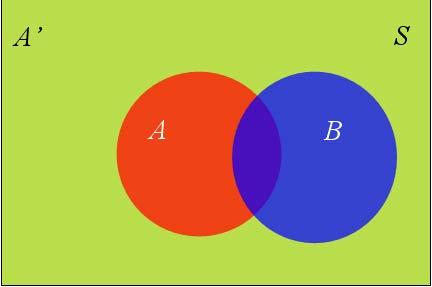

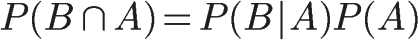
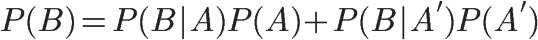
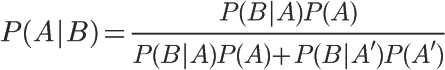
朴素贝叶斯推断
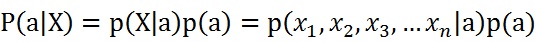
由于每个特征都是独立的,我们可以进一步拆分公式: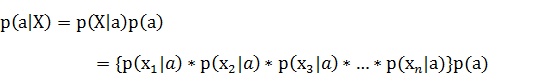
实践
朴素贝叶斯
https://github.com/zdkswd/MLcode/blob/master/%E7%AE%97%E6%B3%95%E5%AE%9E%E7%8E%B0/bayes.py
sklearn-朴素贝叶斯
在sklearn中一共有三个朴素贝叶斯分类算法类。分别是GaussianNB,MultinomialNB和BernoulliNB。其中GaussianNB就是先验为高斯分布的朴素贝叶斯,MultinomialNB就是先验为多项式分布的朴素贝叶斯,而BernoulliNB就是先验为伯努利分布的朴素贝叶斯。
对于新闻分类,属于多分类问题。我们可以使用MultinamialNB()完成我们的新闻分类问题。MultinomialNB假设特征的先验概率为多项式分布,即如下式: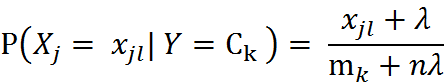
其中, P(Xj = Xjl | Y = Ck)是第k个类别的第j维特征的第l个取值条件概率。mk是训练集中输出为第k类的样本个数。λ为一个大于0的常数,常常取值为1,即拉普拉斯平滑,也可以取其他值。
MultinamialNB这个函数,只有3个参数:
参数说明如下:
- alpha:浮点型可选参数,默认为1.0,其实就是添加拉普拉斯平滑,即为上述公式中的λ ,如果这个参数设置为0,就是不添加平滑;
- fit_prior:布尔型可选参数,默认为True。布尔参数fit_prior表示是否要考虑先验概率,如果是false,则所有的样本类别输出都有相同的类别先验概率。否则可以自己用第三个参数class_prior输入先验概率,或者不输入第三个参数class_prior让MultinomialNB自己从训练集样本来计算先验概率,此时的先验概率为P(Y=Ck)=mk/m。其中m为训练集样本总数量,mk为输出为第k类别的训练集样本数。
- class_prior:可选参数,默认为None。

MultinomialNB一个重要的功能是有partial_fit方法,这个方法的一般用在如果训练集数据量非常大,一次不能全部载入内存的时候。这时我们可以把训练集分成若干等分,重复调用partial_fit来一步步的学习训练集,非常方便。GaussianNB和BernoulliNB也有类似的功能。 在使用MultinomialNB的fit方法或者partial_fit方法拟合数据后,我们可以进行预测。此时预测有三种方法,包括predict,predict_log_proba和predict_proba。predict方法就是我们最常用的预测方法,直接给出测试集的预测类别输出。predict_proba则不同,它会给出测试集样本在各个类别上预测的概率。容易理解,predict_proba预测出的各个类别概率里的最大值对应的类别,也就是predict方法得到类别。predict_log_proba和predict_proba类似,它会给出测试集样本在各个类别上预测的概率的一个对数转化。转化后predict_log_proba预测出的各个类别对数概率里的最大值对应的类别,也就是predict方法得到类别。